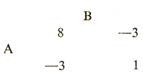Game Theory: Assumptions, Application and Limitations!
John Von Neumann and Oscar Morgenstern are considered to be the originator of game theory. They mentioned it in the book ‘Theory of Games and Economic Behaviour’. A game is a situation in which two or more participants take part in pursuit of certain conflicting objectives.
ADVERTISEMENTS:
In this case, some players may win by getting positive gain while others may lose. In the same way in competitive market, two or more parties make decisions with conflicting interest and action of one depends on the opponent task. Each and every opponent ‘acts in rational way for resolving the conflicting in own favour.
Game theory resolves this conflicting situation of business and military operations. This important technique of operation research provides a basis for determining under specified conditions, the particular strategy that will result in maximum gain or minimum loss. Thus game theory may be defined as a body of knowledge that deals the decision making of two or more rational opponents in the condition of conflict and competition.
Assumptions:
1. The number of players (competitors) in finite.
2. All players act rationally and intelligently.
ADVERTISEMENTS:
3. Each player has a definite course of action.
4. There is conflict of interest between the players.
5. The rules of play are known to all the players.
The zero sums two person games:
In a zero sum game the gain of one player is the loss of the other so that the total of gains and losses is always equal to zero. For example, when two firms compete in a duopolistic market the gain of one will be the loss of other. The contest involves in attracting the customers, then the number of customers gained by one firm must be same as number of customers lost by the other. This is two person zero sum game.
ADVERTISEMENTS:
In the case of duopoly, assume two firms A and B are competing. Firm A has availability of three strategies A1, A2 and A3. Firm B has four strategies B1, B2, B3 and B4. If we consider any pair of strategies, e.g. A opt for strategy A2 and B opt for B3 it results in 7 per cent gain of market share for A and same loss for B.
In this way the payoff matrix can be achieved in the form of table. The strategies and their corresponding payoff matrix are given in the following table:
If firm A selects the strategy Ax, then B will reply by selecting minimum value of B1, B2, B3 and B4 i.e. B3, for minimum payoff to A. Row minima and column maxima is selected. After this max min and mini max principle is followed and sadle point is decided. In brief, the following procedure is adopted.
ADVERTISEMENTS:
(a) Find the minimum value in each row.
(b) The max min value is calculated of the minimum value (that is 16).
(c) Find the maximum value of each column.
(d) The mini max value is calculated of the maximum value (that is 16).
ADVERTISEMENTS:
(e) Sadie point is that where the mini max and max min coincides (that is 16).
Thus the optimum solution to the game is:
(i) The best strategy for firm A is A1.
(ii) The best strategy for firm B is B3, and
ADVERTISEMENTS:
(iii) The value of the game is 16 for firm A and—16 for firm B.
In some games the max min and mini max value does not coincide. Therefore, saddle point is not existing, There are two methods: graphical and linear programming for solving this case.
Illustration:
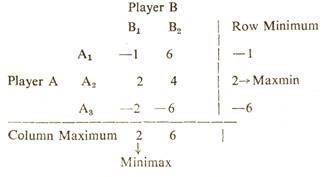
Player A can choose his strategies from A1, A2, A3 only while player B can choose from B1, B2 only. The rules of game state that the payments should be made in accordance with the selection of strategies:
What strategies should A and B plays in order to get the optimal benefit of the play?
ADVERTISEMENTS:
We can display the payment in the following payoff matrix for player A.
The matrix has a saddle point at position A2, B1. The optimal solution to the game is:
(i) Best strategy for player A is A2
(ii) Best strategy for player B is B1 and
ADVERTISEMENTS:
(iii) The value of the game is Rs. 2 for player A and Rs. —2 for player B.
Mixed strategies:
If the mini max and max min value does not coincides, it is said the case of mixed strategy. Then the problem of game theory is solved by probability theory.
Solve the following game and determine the value of the game:
The payoff matrix does not possess any saddle point. The players will use mixed strategies. In this case of matrix [ab/ cd] the following formulae is used
R= a + d-b-c
ADVERTISEMENTS:
R= 8+1+3+3=15
Value of the game will be
V= (ad-bc)/R
= [8 x 1 – (-3 x -3)]/ 15
= (8-9)/ 15 = – 1/15
Probability for A will be
ADVERTISEMENTS:
P1= (d-c)/ R or (1+3)/15 or 4/15
Probability for B will be
P2= (a-b)/ R or (8+3)/15 or 11/15
Applications:
The game theory can be applied to decide the best course in conflicting situations. In business decisions it has wider possibilities. With the help of computer large number of independent variables can be considered with mathematical accuracy. The main advantages of this theory are:
1. Game theory provides a systematic quantitative approach for deciding the best strategy in competitive situations.
2. It provides a framework for competitor’s reactions to the firm actions.
ADVERTISEMENTS:
3. It is helpful in handling the situation of independence of firms.
4. Game theory is a management device which helps rational decision-making.
Limitations:
1. As the number of players increases in the actual business the game theory becomes more difficult.
2. It simply provides a general rule of logic not the winning strategy.
3. There is much uncertainty in actual field of business which cannot be considered in game theory.
4. Businessmen do not have adequate knowledge for the game theory.