Capital Budgeting: Meaning, Definitions, Techniques, Methods and Process

Capital budgeting is a process which helps enterprises in examining the financial implications of the long term investment projects. The decision of accepting or rejecting an investment project as part of a company’s policy depends upon the investment rate of return that such a project will generate.

Capital budgeting is the process of evaluating and selecting investments in capital assets or fixed assets in a firm. Capital budgeting is vital in achieving the shareholders’ wealth maximisation objective of a firm.

In recent years, there has been a lot of technical literature, including articles by Joel Dean, Ezra Solomon, Larie, Savage and Jack Hirshleifer. The term capital budgeting contains two words-capital, the relatively scarce, non-human resource of production enterprise, and budgeting thus indicating a detailed, quantified planning which guides future activities of an enterprise towards the achievement of its profit goals.

Capital budgeting may be defined as the decision-making process by which a firm evaluates the purchase of major fixed assets, including buildings, machinery and equipment. It deals exclusively with major investment proposals which are essentially long-term projects and is concerned with the allocation of the firm’s scarce financial resources among the available market opportunities.

Contents

An Overview of Capital Budgeting
Introduction to Capital Budgeting
Meaning of Capital Budgeting
Definitions of Capital Budgeting
Concept of Capital Budgeting
Nature of Capital Budgeting
Capital Budgeting Decisions
Objectives of Capital Budgeting
Characteristics of Capital Budgeting
Importance of Capital Budgeting
Significance of Capital Budgeting
Kinds of Capital Budgeting Proposals
Types of Capital Budgeting Decisions Taken by a Firm
Techniques of Capital Budgeting
Methods of Capital Budgeting
Requirements of an Ideal Method of Investment Decision Making
Stages Involved in Capital Budgeting Process
Steps Involved in Capital Budgeting Process
Capital Budgeting Decisions
Analysis of Risk and Uncertainty under Capital Budgeting
Complex Situations in Capital Budgeting
Risk Analysis in Capital Budgeting
Investment Decision
Capital Rationing
Appraisal of Capital Budgeting Proposals
Fallacies in Analysing Capital Budgeting Proposals
Fundamentals of Evaluating Foreign Projects
Tax Implications on Capital Budgeting
Capital Budgeting in Practice
Problems in Capital Budgeting
Limitations of Capital Budgeting

Capital Budgeting: Meaning, Definitions, Objectives, Importance, Types, Techniques, Methods, Process, Importance, Decisions, Risk Analysis and More…

Capital Budgeting – An Overview

Among the various finance functions, one of the most important decisions is pertaining to investment of funds for a long period of time. All enterprises are required to take a long term decision to sustain or to enhance their profitability.

These decisions are not taken very frequently by the organisation as they involve huge amounts of funds and the effects of the investment have bearing on the profitability for a long period of time.

Therefore, it is imperative for a financial manager to take these decisions very cautiously. According to Lynch, “Capital Budgeting consists in planning the development of available capital for the purpose of maximizing long term profitability of the concern.”

The rate of return generated by the project is influenced by other factors that are specific to the company as well as the project. For example, the acceptance or rejection of a social or charitable project is not solely based on quantitative return estimated in the process but also takes into consideration other issues such as contribution to foster goodwill and fulfillment of corporate responsibility norms.

Since Capital budgeting involves investment of a huge amount of funds, it is necessary to understand the risks and returns involved otherwise the finance manager would be criticized by its owners or shareholders. An imperfect or casual approach in measuring the effectiveness of these decisions would create difficulty for survival of enterprises.

Capital Budgeting – Introduction

In capital budgeting, we estimate the future cash flows and make the investment, only if the present value of cash inflows exceeds the investment’s cost or cash inflows yield a return equal to the required rate of return on the capital.

The capital budgeting may involve selecting investments in starting of business, modernisation of business, replacement of existing fixed assets, expansion of business or in diversification of business. Merger and acquisition is also a capital budgeting decision for the acquiring firm.

For example- investing in a cycle manufacturing unit involves a capital budgeting decision. Here, future cash flows are estimated and if they yield a return required to meet the cost of capital (the return required by those financing the project) the investment in the cycle manufacturing unit is desirable.

Capital budgeting may involve evaluating a number of projects simultaneously and selecting the most suitable from these projects.

The cost of capital (the return required by those financing the project) and estimation of future cash inflows are two main considerations in making capital budgeting. The capital budgeting is also known as capital expenditure decision, capital expenditure management, management of fixed assets, long-term decision etc.

The finance manager of a firm is responsible to procure the required quantum of funds from different sources and invest the raised funds in various assets in the most profitable way. The investment of funds requires a number of decisions to be taken in a situation in which funds are invested and benefits are expected over a long period.

The finance manager is to determine the composition of assets of the firm. The assets of the firm are of two types i.e., fixed assets and current assets. The aspect of taking the financial decision with regard to fixed assets is called capital budgeting.

Capital Budgeting – Meaning

Palmer and Taylor state that probably more words have been written on the subject of capital budgeting in recent years than on any other subject relating to financial planning and control in business. Decades ago, economists Bohn-Bawerk, Wicksell and Irving Fisher laid the theoretical foundation for a sound economic approach to capital budgeting.

‘Capital’ relates to total funds employed in an enterprise as a whole. The capital fund is increased by an inward flow of cash and decreased by an outward flow of cash and as such it is important for an enterprise to plan and arrange cash flows properly.

The power of the financial planning package lies in enabling borrowings to be arranged sufficiently in advance to reduce the danger of a liquidity crisis as also to provide substantiating documents for loan negotiations.

Capital budgeting then consists in planning the deployment of available capital for the purpose of maximising the long-term profitability (return on investment) of a firm. It refers to the process by which a firm determines where it should apply its comparatively limited financial resources.

It is a many-sided activity which includes a search for a new and more profitable investment proposal and the making of an economic analysis to determine the profit potential of each investment proposal.

The term ‘capital expenditure projects’ is broad enough to include those projects in which the net assets of a company are acquired by the issue of the capital stock of the acquiring company. Capital budgeting involves a long-term planning for making and financing proposed capital outlays.

Most expenditures for long-lived assets affect a firm’s operations over a period of time (years). They are large, permanent commitments which influence its long-run flexibility and earning power.

It is a process by which available cash and credit resources are allocated among competitive long-term investment opportunities so as to promote the greatest profitability of a company over a period of time. It refers to the total process of generating, evaluating, selecting and following up on capital expenditure alternatives.

Definitions of Capital Budgeting

There are two types of expenditures generally made in a business viz. Capital Expenditure and Revenue Expenditure. Revenue expenditure is required for day to day operating requirements whereas Capital expenditure is incurred in making investment in fixed assets.

Following are some of its important definitions:

“Capital budgeting is long-term planning for making and financing proposed capital outlays.” — Charles T. Horngren

“Capital budgeting involves the planning of expenditures for assets the returns from which will be realized in future time periods.” — Milton H. Spencer

“Capital budgeting is concerned with the allocation of the firm’s source financial resources among the available opportunities. The consideration of investment opportunities involves the comparison of the expected future streams of earnings from a project with the immediate and subsequent streams of earnings from a project, with the immediate and subsequent streams of expenditure”. — GC. Philippatos,

“Capital budgeting is acquiring inputs with long-term return”. —Richard and Green law “Capital budgeting consists in planning the development of available capital for the purpose of maximizing the long-term profitability (return on investment) of the firm.” — R. M. Lynch

Concept of Capital Budgeting

A business firm is created by entrepreneurs because they see an opportunity for profitable investment. They estimate the total requirement of funds to be invested in both long-term as well as short-term assets of the firm.

The efficient allocation of funds particularly in long-term assets by a firm is of vital importance for the realisation of its objective. In this era of globalisation, even the existing businesses face a lot of competition to survive in the volatile environment. Every firm has to meet the challenges coming up in its way.

Therefore, it has to adapt to the new technology, plants, machineries, products, methods etc. and have to incur capital expenditure for the purpose of surviving in this competitive environment.

Hence, every business, whether new or existing, has to invest a lot of its scarce funds in long-term assets. The investment decisions involving commitment of current funds of the firm in its long-term assets are known as capital budgeting or capital expenditure decisions, expenditure decisions.

Long-term assets are those which are used by the firm for a longer period, usually beyond one year. Therefore, investment in capital assets (long-term assets) benefits a firm over a longer period of time.

Nature of Capital Budgeting

Nature of Capital Budgeting:

1. Huge investments

Capital budgeting requires huge investments of funds, but the available funds are limited, therefore the firm before investing projects, plan are control its capital expenditure.

2. Long-term

Capital expenditure is long-term in nature or permanent in nature. Therefore financial risks involved in the investment decision are more. If higher risks are involved, it needs careful planning of capital budgeting.

3. Irreversible

The capital investment decisions are irreversible, are not changed back. Once the decision is taken for purchasing a permanent asset, it is very difficult to dispose of those assets without involving huge losses.

4. Long-term effect

Capital budgeting not only reduces the cost but also increases the revenue in the long-term and will bring significant changes in the profit of the company by avoiding over or more investment or under investment.

Over investments leads to be unable to utilize assets or over utilization of fixed assets. Therefore before making the investment, careful planning and analysis of the project thoroughly is required.

Capital Budgeting Decisions

Broadly speaking, capital budgeting decisions are long-term investment decisions.

They include the following:

1. Expansion Decisions

Decisions on matters such as acquisition of new machinery or building, addition of building and machinery etc. are taken on the basis of cost of investment and expected profits from goods produced.

2. Replacement Decisions

A company may have to replace its existing old or obsolete machinery by new and latest model machinery. The use of new machinery may bring down operating costs and increase the volume of output. Decisions on such matters are taken on the basis of saving on account of decrease in operating costs and profits from additional volume produced by new plants.

3. Buy or Lease Decisions

The management may have to take decision on acquiring a fixed asset by purchasing it from the market or by arranging it on lease basis. Such decisions are taken by comparing the cost of funds required for the purchase of assets with the amount payable on lease.

4. Choice of Equipment

The management may have to select the best machine out of available several alternative machines. Decisions on such matters are taken by comparing the cost of different assets with their respective profitability.

5. Product of Process Improvement

This concern with decisions on matters related to cost reduction or improvement in the quality of product by change in production processes. Decision on such matters is taken on the basis of a comparative study of cost of change and possible additional income or saving as a result of change.

Objectives of Capital Budgeting

The objectives of capital budgeting are:

1. To decide whether a specified project is to be selected or not.

2. To find out the quantum of finance required for the capital expenditure.

3. To evaluate the merits of each proposal to decide which project is best.

4. Improving quality of products and creating new demand.

5. Expansion of existing business.

6. Diversification for survival particularly in competitive conditions.

7. Improvement of efficiency.

8. Meeting satisfaction of customers.

Characteristics of Capital Budgeting

Capital Expenditure for Long Period:

Capital budgeting entails heavy expenditure. Infact, this is a very important characteristic which explains the importance of capital budgeting decisions to a firm. Capital is sunk for a long period. This long-term commitment adds considerably to the risk of capital budgeting decisions.

Capital expenditure is the main link between the present and the future, for it is the principal means by which an industrial company tries to attain its long-term goals and objectives.

Because of its relationship with long-term profit planning, its disproportionately heavy impact on short-term profits and its high volume, capital expenditure should be planned and controlled. Decisions which involve the authorisation of capital expenditure projects are among the most important for the Boards of Directors and their managerial advisers.

Most capital expenditure schemes call for a permanent commitment of relatively large sums of money over a number of years. Capital expenditure is strategic investment of some magnitude and is of a non-routine nature; it has economic life and its benefits continue over a series of years.

From the standpoint of the stockholder and the consumer, capital expenditures are the principal bulwark against the seemingly endless progression of wage increase. From the standpoint of labour, capital expenditures are the basic economic source of future wage advances, for they embody the creative forward strides of advancing technology.

Finally, capital expenditures, both by their aggregate size and by their cyclical timing, have a great deal to do with the character of the economy as a whole, and therefore, with the government’s role in maintaining stability-

(i) Creative Search for Profitable Opportunities

The concept of the profit-making idea must be embodied in the capital facility. Profitable opportunities for the company’s invested capital must be turned up. A corporation’s future profitability and growth are linked to the soundness of its capital expenditure policy.

This calls for the need for clearly identifying the steps of a capital expenditure management programme. These steps then require to be integrated into a procedure to be used for the conduct of an organisation’s capital expenditure programme.

(ii) Long-range Capital Planning

To provide consistent benchmarks for proposal origination in all parts of the organisation, it is necessary to have some kind of a plan sketched for the future even though it is a tentative plan. Consider the words of Joel Dean, “Today’s capital expenditures make the bed that the company must lie in tomorrow. The capital expenditure budget embraces a company’s plans for replacing, improving and adding to its capital equipment”.

(iii) Short-range Capital Planning

The purpose of preparing a short-range capital budget is to force the operating management to submit the bulk of its capital proposals early enough to give the top management an indication of the company’s credit demands for funds.

(iv) Measurement of Project Worth

In order to permit an objective ranging of projects, the productivity of the proposed outlay will have to be measured properly.

(v) Screening and Selection

A screening standard should be set in the light of the supply of cash available for capital expenditures, the cost of money to the company, and the attractiveness of alternative investment opportunities.

(vi) Control of Authorised Outlays

Control has to be exercised by the top management in order to ensure that the facility conforms to specifications and that the outlay does not exceed the amount authorised. Once the capital expenditure is incurred, it is most difficult to change the course of expenditure. As capital assets are usually of limited specific use, the future needs of such assets should be carefully assessed.

(vii) Post Mortem

In order to preserve the integration of the estimates of projected earnings, a post-completion audit of the company’s performance should be effected.

(viii) Retirement and Disposal

A management’s responsibility for an investment approach ceases only when the facilities have been disposed of. The asset must be retained throughout its economic life until it virtually becomes worthless at the time of disposal.

(ix) Forms and Procedures

An effective system of capital expenditure control should be implemented with the use of specialised forms, written procedures etc. all tailored to the company’s needs.

(x) Economics of Capital budgeting

Good estimates of a rate of return of capital expenditure projects pre-suppose an understanding of the economic concepts that underlie sound investment decisions.

(xi) Increase the Breadth of Analysis Leading to Decision-Making

In evaluating capital expenditure decisions or a profit-plan, it has been fairly common to consider only a few alternative strategies or economic assumptions before reaching a decision.

(xii) Tool for Special Problems

More and more attention is being devoted by management to temporary and special problem situations.

(xiii) Understanding inherent Logic of the Financial System

As a by-product of financial modelling, some executives have found that the act of defining the logic and interaction of the financial system in developing the model is, in itself, a very important and revealing activity.

Forecasting:

As funds are committed over extended periods of time, there is a need for proper forecasting. A bird in hand is worth two in the bush. There is an element of uncertainty and risk which may lie in store for the future. All these factors have to be properly evaluated in the process of forecasting. A proper cost-benefit relationship should also be established.

Planning Asset Capacities:

A firm has to assess the capacities of the assets properly before arriving at its long-term decisions. Both under-capacities and over-capacities should be avoided. Moreover, the management should determine the timing and the quality of asset acquisitions.

Asset capacities have to be related to market factors, which may change over a period of time because of various cyclical fluctuations. A firm should, therefore, plan and fix the capacities of its assets in which long-term investment is going to be sunk.

Far-sighted judgement is an essential prerequisite of wise decisions bearing on capital expenditures. But much judgement, to be sound, should be based on an analysis of all the facts, many of which may be extremely technical and complex.

The top management needs an objective means of measuring the economic worth of individual investment proposals so that it may choose and select those which will have the most profound impact on a company’s long-run prosperity.

The real worth of an investment proposal may be traced to the credibility of the forecasts of the sales demand and production capacity which underpin the validity of the assessments and any miscalculation of these is likely to be of far greater consequence than the relatively marginal effects of errors caused by the use of a wrong rate of interest in discounting calculations.

Importance of Capital Budgeting

Importance of Capital Budgeting:

Importance # 1. Long-term Implications

A Capital budgeting decision has its effect over a long time span and inevitably affects the company’s future cost structure and growth. A wrong decision can prove disastrous for the long term survival of the firm.

It leads to unwanted expansion of assets which results in heavy operating cost to the firm. On the other hand, lack of investment in assets would influence the competitive position of the firm. So the capital budgeting decision determines the future density of the company.

Importance # 2. Involvement of Large Amount of Fund

Capital budgeting decisions need substantial amounts of capital outlay. This underlines the need for thoughtful, wise and correct decisions as an incorrect decision would not only result in losses but also prevent the firm from earning profit from other investments which could not be undertaken.

Importance # 3. Irreversible Decisions

Capital budgeting decisions in most of the cases are irreversible because it is difficult to find a market for such assets. Then the only way out will be to scrap the capital assets. So acquired and incur heavy losses.

Importance # 4. Risk and Uncertainty

Capital budgeting decisions are surrounded by a great number of uncertainties. Investment is present and investment is future. The future is uncertain and full of risks. Longer the period of project, greater may be the risk and uncertainty. The estimates about cost revenues profits may not come true.

Significance of Capital Budgeting

Significance of Capital Budgeting:

The significance of capital budgeting can be emphasized taking into consideration the very nature of the capital expenditure such as huge investment in capital projects, long-term implications for the firm, irreversible decisions and complications of the decision making.

The significance of capital budgeting can be summarized as follows:

(1) Indirect Forecast of Sales:

The investment in fixed assets is related to future sales of the firm during the lifetime of the assets purchased. It shows the possibility of expanding the production facilities to cover additional sales shown in the sales budget.

Any failure to make the sales forecast accurately would result in over investment or under investment in fixed assets and any erroneous forecast of asset needs may lead the firm to serious economic results.

(2) Comparative Study of Alternative Projects:

Capital budgeting makes a comparative study of the alternative projects for the replacement of assets which are wearing out or are in danger of becoming obsolete so as to make the best possible investment in the replacement of assets. For this purpose, the profitability of each project is estimated.

(3) Timing of Assets-Acquisition:

Proper capital budgeting leads to proper timing of assets-acquisition and improvement in the quality of assets purchased.

Due to the nature of demand and supply of capital goods, the demand of capital goods does not arise until sales impinge on productive capacity and such situations occur only intermittently. On the other hand, supply of capital goods with their availability is one of the functions of capital budgeting.

(4) Cash Forecast:

Capital investment requires substantial funds which can only be arranged by making determined efforts to ensure their availability at the right time. Thus it facilitates a cash forecast.

(5) Wealth-Maximization of Shareholders:

The impact of long-term capital investment decisions is far reaching. It protects the interests of the shareholders and of the enterprise because it avoids over-investment and under-investment in fixed assets.

By selecting the most profitable projects, the management facilitates the wealth maximization of the equity share-holders.

Kinds of Capital Budgeting Proposals

Kinds of capital budgeting proposals are given below:

1. Replacements

Worn-out, obsolete equipment should be replaced at an appropriate time.

2. Expansion

If the product is in great demand, a firm may think of expanding its activities. Expansion involves an addition of capacity to the existing production facilities. The proposal would then include capital widening decisions and assist in the dynamic growth of the firm. Qualitative efforts should be made to increase the existing utilisation of capacity.

3. Modernisation of Investment Expenditures

These are capital-deep decisions. They make it easier for a firm to reduce costs and may coincide with replacement decisions.

4. Strategic Investment Proposals

There are capital budgeting decisions which do not assume that the return would be immediate or be measured over a long period of time. Strategic investments may be defensive, offensive and mixed-motive decisions.

The vertical integration of a firm is an example of a defensive investment in which a continuous source of raw materials is assured. Horizontal and conglomerate combinations are offensive investments, for they ensure a firm’s internal and external growth respectively. Mixed motive investments are outlays on research and development programmes.

5. Diversification

Diversification means operating in several markets or from one market into another market. It may even amount to changing product lines. A firm resorts to diversification to ensure breakeven risks involved in different products lines.

6. Research and Development

Where technology is rapidly changing, research and development becomes a continuous activity for any firm. Usually, large sums of money are invested in ‘R & D’ activities which lead to capital budgeting decisions.

Harold Bierman and Seymour Smidt classify investments as follows:

(a) On the basis of the kinds of scarce resources used or required;

(b) According to the amount of each of the resources that are required;

(d) According to the form in which benefits are received;

(e) Whether incremental benefits are the result of lower costs or increased sales-whether they merely prevent a decline in sales or market share;

(f) According to the business activity to which they are most closely related.

They are of the opinion that no single scheme of classification is equally valid for all the uses or for all the companies. The essential task is to develop a classification system for investment that is appropriate to the activity of the business and the organisational structure of the particular company.

Types of Capital Budgeting Decisions Taken by a Firm

Capital budgeting decisions are concerned with a number of issues related to a firm. It may be set up of a new business, modernisation of business or the other.

The following types of capital budgeting decisions are taken by a firm:

1. Set up of new business

The setting up of a business involves large capital investment. The decision to start a business is simply a capital budgeting decision.

2. Modernisation

To remain in business, a firm may require modernisation from time to time. Modernisation may involve huge investment in long-term assets. Capital budgeting decisions are taken in such a case.

3. Replacement

A capital budgeting decision may be related to replacement of an existing machinery or equipment in a firm. The replacement of machinery or equipment may be needed on account of a number of factors, like to increase the efficiency, obsolescence, cost saving etc.

4. Expansion

A firm doing good business may be interested in expanding the production capacity to capture more market share. Capital budgeting is necessary to evaluate the expansion and decide about the execution of expansion.

5. Diversification

The existing firms may be interested in diversifying their business by introducing new product lines to increase their product base. Before executing any such move, a firm has to make a capital budgeting decision.

6. Acquisition

In an acquisition, one firm buys another one. This is different from buying machinery or starting a new firm. The same principles of capital budgeting are involved in acquisition analysis.

Capital Budgeting Techniques

The following are the techniques which are found to be in general use:

Technique # 1. Payback Method:

The payback method is based on the assumption that the degree of risk associated with the fixed asset is the length of time required to recover the investment from the firm’s cash flow. The payback period is defined as the length of time required for the stream of cash proceeds produced by an investment to equal the original cash outlay required by the investment.

This method is also known as the pay-out method:

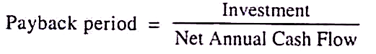
Thus, the payback period is the length of time required to recover an initial fixed investment through returning cash flow. This flow includes both the depreciation recoveries and the net income after taxes.

The recovery of invested principal as rapidly as possible reduces the amount of capital devoted to a project. It also reduces the risk of possible loss of the capital.

Advantages:

(i) It is an important guide to investment policy,

(ii) It lays a great emphasis on liquidity,

(iii) The rate at which capital is recouped has a positive significance,

(iv) It is easy to understand, calculate and communicate to the other,

(v) The method enables a firm to choose an investment which yields a quick return on cash funds,

(vi) It enables a firm to determine the period required to recover the original investment with some percentage return and thus arrive at the degree of risk associated with the investment,

(vii) It emphasises the liquidity and solvency of a firm, which is undoubtedly an important consideration,

(viii) It is an adequate measure, with very profitable internal investment opportunities,

(ix) It weighs early returns heavily and ignores distant returns. It thus contains a built-in hedge against economic depreciation or obsolescence,

(x) When the payback index is used for ranking competitive projects, it has the advantage of eliminating any bias due to project size in terms of cost,

(xi) The method is quite the simplest of all the techniques used by the industry. It helps in the selection of those projects whose profits are high enough to repay the amount invested within a particular number of years,

(xii) Other than its simplicity, the main advantage claimed for the payback method is that it is a built-in safeguard against risk.

Disadvantages:

(i) It does not measure the profitability of a project,

(ii) The timing of the flow is not considered a vital factor,

(iii) The time value of money is ignored,

(iv) The rapidity of incoming cash flow is the only measure of desirability,

(v) The rate of expected return is considered in a haphazard manner.

(vi) There is no recognition of cash flow variation. One project may have a cash inflow of Rs.6,000 for the first year, Rs.8,000 for the second year and Rs.10,000 for the third year. The second project may have cash flow of Rs.10,000, Rs.8,000 and Rs.6,000 for three years respectively.

If both the projects involved net cash outlays of Rs.24,000, the payback period would be three years for each. It should be remembered, however, that the second project would yield more cash earlier and may, therefore, be considered more valuable. This situation is not properly handled under the payback method.

(vii) Inadequate effort is made either to ascertain the relative merit of alternative opportunities or to maximise profits,

(viii) It does not value projects of different economic lives. The economic life of a project is the life beyond the payback period. The payback method considers only the payback period of the proposals, and does not consider the period beyond that.

Infact, a project which has a longer life beyond the payback period is more economical than the one which enjoys a shorter life period beyond the payback period. One obvious shortcoming of the payback index is that most projects continue to generate the cash flow beyond the payback period; its exclusion from consideration may, therefore, create a wrong impression as to the relative desirability of several competing projects,

(ix) It does not consider income beyond the payback period and looks upon it as a windfall,

(x) It includes the cost of capital, does not relate to productivity, and emphasises only time dimensions,

(xi) It does not indicate how to maximise value and ignores the relative profitability of the project,

(xii) It is useful for certain firms only. Its generality, therefore, is severely constrained,

(xiii) It over-emphasizes liquidity and ignores capital wastage and the economic life of an asset,

(xiv) It is only a rule-of-thumb method. It is often difficult to judge objectively whether one proposed project is superior to another and, if so, by how much,

(xv) The payback concept does not reflect all the relevant dimensions of profitability. In especially risky situations, therefore, it is not sufficiently inclusive or payback sensitive enough to be used as a measure of investment worth,

(xvi) The method is often criticised on the ground that it does not take into consideration the concept of the cost of capital which is important for capital budgeting decisions,

(xvii) No allowance is made for taxation nor is any capital allowance made,

(xviii) It ignores the fact that projects may have different profit streams after the payback period is over, and may lead to serious under investment,

(xix) It may choose highly risky projects,

(xx) The method is not consistent with the objective of maximising the market value of the firm’s share. It would be consistent with this objective if share values were a function of the payback period of investment projects.

Corrections for Payback Method:

The defects of the payback method may be somewhat cured in the following ways:

i. Modified Payback Method

Profits earned after the payback period are considered.

ii. Reciprocal of Payback

The method is a close approximation of the ‘Time Adjusted Rate of Return’ (TRR), if the earnings are levelled and the estimated life of the project is somewhat more than twice the back period.

iii. Discounted Reciprocal Payback Method

When savings are not levelled, it is better to calculate the payback period by taking into consideration the present value of cash TRR (provided the estimated economic life of the asset is more than twice the payback period). The rate thus calculated slightly overstates the true returns.

The traditional methods (especially the payback method) are not easily preferred when there is a danger of obsolescence due to rapid technological developments and when there is a great shortage of funds and a long list of priority projects.

Big companies in India, however, like to adopt the payback method for the evaluation of capital expenditure proposals. Moreover, in spite of its limitations, if rightly understood, the payback method may serve as a useful screening device before more precise methods are applied.

Technique # 2. Average Rate of Return:

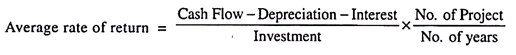
Advantages:

(i) It selects alternative uses of funds,

(ii) It considers savings over the entire life of the project.

(iii) In addition to measuring the desirability of new investments on the basis of their relative cash flows, a comparison is made of expected profitability.

This is done with the average rate of return, which is a ratio of the yearly average net earnings after depreciation and taxes to the average investment.

Disadvantages:

(i) The differential timing of receipts is not considered,

(ii) It ignores the time value of funds.

Technique # 3. Internal Rate of Return:

The internal rate of return is the rate which equates the present value of the expected future cash flows with the cost of the investment. The rate of discount is determined by the trial-and-error method to bring the present value of the projects close to the investment. Subsequently, the exact internal rate of return is estimated with the help of interpolation.

The discounted cash flow return is thus nothing but a true annual rate of return of the capital outstanding in the investment. The implicit discount rate-the expected rate of total return that equilibrates current price with a forecast dividend stream-is the single most important piece of information to have about a common stock.

Risk premiums and liquidity preference premiums play a pivotal role in explaining variations in the discount rate. Although these premiums are constantly changing, the effect of changes on the structure of implicit discount rates is systematic.

In particular, it is usually true that

(i) The higher the market risk of a stock, the higher the discount rate or expected return tends to be; and

(ii) The lower the market liquidity, the higher the discount rate or expected return tends to be.

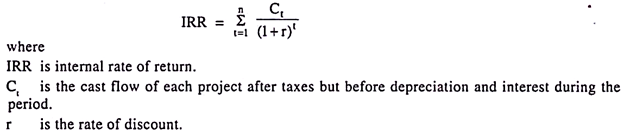
Advantages:

(i) It measures the relative profitability of an investment on the basis of a single overall rate of return per year.

(ii) It diverges according to the goals of the firm. It can be used to accept a combination of projects.

(iii) It enables a firm to choose from among different alternatives.

(iv) It enables a firm to know the rate of return which it would receive discounted over a period of years required to recover the original investment.

(v) It restricts investment expenditure to the amount of funds internally generated by a firm. In its simplest form, it refers to the supply and cost of finance.

Disadvantages:

(i) Although a simple operation, the computation becomes quite tedious.

(ii) Accounting Information – It uses accounting information and does not explain the cash flow position.

(iii) Ignores Time Value of Money – It ignores the time of receipts and expenses. It does not make use of the time value of money in investment decisions.

(iv) Multiple Concepts of Investments – There is no full agreement on the accurate measure of the term ‘investment’. This rate of return, therefore, becomes unreliable.

Technique # 4. Net Present Worth:

A business firm has a positive preference for the time factor. It prefers to present goods to the same quantity of commodities in the future. The present is here and now, and is more certain than the future.

The financial manager places a greater value on present funds than on future funds because:

(i) The additional income is available now rather than in the future;

(ii) There is a greater certainty associated with present assets;

(iii) Future receipts are only current estimates;

(iv) A risk is involved in future receipts.

There are two aspects of this problem. One is the annuity principle and the other is the present value of future income.

According to the annuity principle:

This method calculates the net present worth of the expected net cash flows of each project, which is obtained by discounting the net cash flows of each project by a discount rate which equals the firm’s cost of capital.

The net present value method is a classic economic method of investment appraisal. While it is favoured by a majority of economists, it has not found much support elsewhere. In business, the discounted cash flow method is generally preferred.

Net cash flows are the incremental cash receipts, less the incremental expenditures solely attributable to the decision to proceed with an investment.

The present value of an investment may be described as the investment without being financially worse off:

Solution:

It is obvious that the new project value of project X exceeds that of project Y by Rs.189.76. The management would naturally prefer project X to project Y, if the projects are mutually exclusive.

Advantages:

(i) The net present value method computes the discount rate at the cost of capital,

(ii) It is useful for simple ‘accept’ or ‘reject’ type;

(iii) The present value method is superior to other methods of evaluating the economic worth of investments,

(iv) The net present value method is generally accepted by economists. Hawkins and Pearce state that this method “is theoretically unassailable. If one wishes to maximise profits, the use of NPV always finds the correct collection of projects.”

(v) The concept of the present value of a series of cash flows is an important feature of the analysis of different investment potentialities. The net present worth technique analyses the merit or relative capital investments. It estimates the present value of their cash flows by using a discount rate equal to the current estimated percentage cost of capital.

Disadvantages:

(i) It gives the same decision for mutually exclusive projects as the discounted benefit-cost ratio.

(ii) It leads to confusing and contradictory answers for the ranking of complicated projects.

Technique # 5. Profitability Index:

The profitability index is the relationship that exists between the present values of net cash inflows and the present values of cash outflows. It is possible to make use of a profitability index while comparing the relative merits of investments proposals and their ranking as to desirability. It relates the present values of net cash flows discounted at various rates of interest of capital cost to the capital expenditures required for a project.

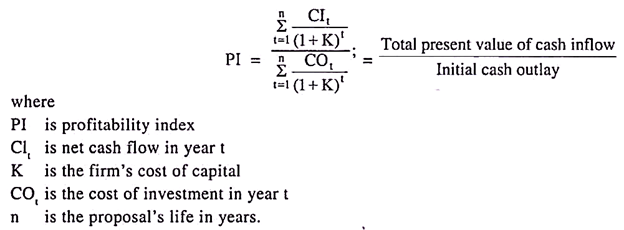
Limitations:

(i) A profitability index of less than one does not indicate losses. It merely means that a firm’s cost of capital exceeds the rates of return. It should not, however, be concluded that the project will lose money, for there may be some other factors which may adequately overcome the slight difference between the cost of capital and the rate of return,

(ii) It is an index number and cannot be reduced to the rate of return,

(iii) It ignores the small percentage differences between projects.

Technique # 6. Adjusted Net Present Value:

This method assumes risk of possible insolvency and availability in earnings available to shareholders. For this purpose, the expected cash flow is substituted by the model cash flow. A financial executive should ascertain the probable distribution of the annual cash flows of the different projects.

Technique # 7. Discounted Benefit-Cost Ratio:

This is a ratio of the present worth of all the future benefits to the present worth of the project outlay, both streams discounted at the same rate. This discounted benefit- cost ratio is the ratio of the present value of future benefits to the present value of the outlays.

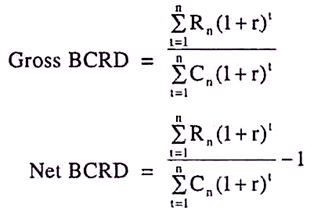
Technique # 8. Undiscounted Benefit-Cost Ratio:

Both benefits and costs are accounted without any discount for futurity, business risk or financial risk.

It is computed with the help of the following formula:

Technique # 9. Net Terminal Value:

Under this method, the cash inflows and outlays are compounded to some future terminal date. If the net terminal value is greater than zero, the project is accepted.

Technique # 10. Annual Benefit-Cost Ratio:

The discounted annual costs are converted into average annual outlays. The latter are compared to the average annual returns. If the gross ratio of annual benefits to the annual costs is greater than unity, the proposal is accepted.

Technique # 11. Net Costs Criterion:

It involves the minimisation of the average cost per unit of product reduced to the present values of the entire productivity of a firm- present and future. It relates directly the cycle of the product demand to the production and investment demand.

Technique # 12. Capital Allocation:

Capital allocation means the way a management arranges assets and claims against assets. The purpose is to achieve the maximum present value for its ownership.

Technique # 13. Cut-Off Point:

The cost of capital is the cut-off point for project selection. A management accepts all the projects with returns exceeding the cost of capital to cut-off, or rejects all those projects with returns exceeding life-time alternative investments-this may differ considerably, and the investor may have a time horizon which is different from any of these in general. What time horizon should be used in the decision rules has no one answer that would apply to all circumstances.

The discounted cash flow methods are sophisticated and can be used with great advantage.

Capital Budgeting Methods

The methods can be grouped into two categories as given below:

Method # I. Traditional (or) Non-discounting Methods

As the name itself suggests, these methods do not discount cash flows to find out their present worth.

There are two such methods available i.e.,

(i) Payback period method, and

(ii) the accounting or average rate of return method.

These are essentially rules of thumb that intuitively grapple with the trade-off between net investment and operating cash inflows.

Both these traditional evaluation criteria are discussed below:

1. Payback Period Method:

This method, sometimes called the payout or pay off or replacement period method, determines the length of time required to recover the initial outlay of a project.

In other words, it is the period within which the total cash inflows from the project equals the cost of investment in the project. The lower the payback period, the better it is since initial investment is recouped faster.

Procedure for computation of payback period:

(i) Ascertain the initial investment (cash outflow) of the project.

(ii) Ascertain the cash inflows (CFAT) from the project for various years.

(iii) Calculate the payback period as under:

(a) In case of uniform CFAT p.a.

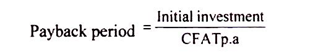
(b) In case of differential CFAT for various years.

(i) Compute cumulative CFAT at the end of each year.

(ii) Find out the year in which cumulative CFAT exceeds initial investment.

(iii) Payback period = Time at which cumulative CFAT = Initial investment (calculated on time proportion basis).

(iv) Accept if the payback period is less than maximum or benchmark period, else reject the project.

Merits of Payback Period Method

(i) It is very easy to apply, calculate and interpret.

(ii) It is most useful when cost is not high and the capital project is completed in a short period.

(iii) It focuses on early return heavily and ignores distant returns. It, thus, contains a built-in edge against economic depreciation or obsolescence.

(iv) It is useful in evaluating those projects which involve high uncertainty.

(v) It considers the liquidity as well as solvency of a firm as a ‘Guiding principle’ in the capital budgeting decisions.

(vi) It gives an indication to a company facing shortage of funds to invest in projects with small payback periods. This is particularly useful when funds are difficult to obtain and a quick return is essential for rapid repayment.

Limitations of Payback Period Method

(i) This method fails to take into account the time value of money. All cash flows are treated and weighed equally regardless of the time period of their occurrence.

(ii) It does not measure the profitability of a project. It ignores the cash inflows beyond the payback period. Thus it is a biased indicator of economic value.

(iii) It does not differentiate between projects requiring different cash investments and thus it does not provide a meaningful and comparable criterion.

(iv) It does not indicate any cut-off period for the purpose of investment decision.

(v) A slight change in operation cost will affect the cash inflows and as such payback period shall also be affected.

(vi) Neither allowance is made for taxation nor is any capital allowance made.

Improvement in traditional approach to payback period

(a) Discounted Payback Period Method:

The payback period method discussed above can be reworked, taking into consideration the time value of money and the firm’s required rate of return, thereby overcoming one of the limitations of the undiscounted payback period method.

When payback period is calculated by taking into account the discount or interest factor, it is known as discounted payback period.

Procedure for calculation of discounted payback period

(i) Ascertain the initial investment (cash outflow).

(ii) Ascertain CFAT (profit before depreciation and after tax) for each year.

(iii) Ascertain the PV factor for each year and compute discounted CFAT (CFAT x PV factor) for each year.

(iv) Ascertain cumulative discounted CFAT at the end of each year.

(v) Ascertain the year in which cumulative discounted CFAT exceeds initial investment.

(v) Calculate discounted payback period at the time at which cumulative discounted CFAT = Initial investment.

(vi) Accept if discounted payback period is less than maximum/benchmark period, else reject the project.

(b) Post pay-back Profitability:

One of the major limitations of the payback period method is that it neglects the profitability of investment during the excess of economic life period over the payback period of that investment.

Hence, an improvement over this method can be made by taking into account the returns receivables beyond the payback period. These returns are called post pay-back profits. If other things remain equal, the project which has the highest post pay-back profits is to be preferred.

The formula for calculating post pay-back profitability index is as follows:

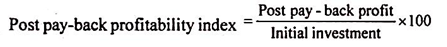
(c) Payback reciprocal:

As the name indicates, it is the reciprocal of payback period. A major limitation of payback period method is that it does not indicate any cut off period for the purpose of investment decision.

It is, however, argued that the reciprocal of the payback would be a close approximation of the internal rate of return if the life of the project is at least twice the payback period and the project generates equal amounts of the annual cash inflow. In practice, the payback reciprocal is a helpful tool for quickly estimating the rate of return of the project provided its life is at least twice the payback period.

The payback reciprocal can be ascertained by using the formula given below:

2. Accounting or Average Rate of Return (ARR) Method

ARR is the annualised net income earned on the average funds invested in a project. It is a measure based on the accounting profit (profit after depreciation and tax) rather than the cash flows and is very similar to the measure of rate of return on capital employed, which is generally used to measure the overall profitability of the firm.

The alternative formula for calculating the ARR is as follows:

where, Annual average net earnings=Average of the earnings (savings) after depreciation and tax over the whole of the economic life of the project.

Investment = Capital cost of the equipment minus salvage value of the old equipment

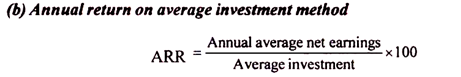
The amount of ‘Average investment’ can be computed in any of the following methods:

Procedure for computation of ARR

(i) Determine the average investment as given above.

(ii) Determine the profit after tax for each year: PAT=CFAT less depreciation.

(iii) Calculate the total PAT for N years, where N = project life.

(iv) Calculate average PAT per annum (Total PAT of all years / N years)

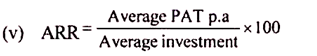
Merits of ARR Method

(i) It is very simple and easy to understand and to use.

(ii) It takes into consideration the total earnings from the project during its lifetime.

(iii) It places emphasis on the profitability of the project, rather than on liquidity as in the case of pay back period method.

(iv) It can be calculated by using the accounting data without another set of workings like cash flow etc.

Demerits of ARR Method

(i) It ignores the time value of money and considers the profit earned in the I^st year as equal to the profits earned in later years. It does not discount the future profits.

(ii) It does not consider the length of project life.

(iii) It ignores the salvage value of the proposal. In real sense, the salvage value is also a return from the proposal and should be considered.

(iv) It also fails to recognise the size of investment required for the project particularly, in case of mutually exclusive proposals, the two projects having significantly different initial costs, may have the same ARR.

Method # II. Discounted Cash Flow (DCF) Methods (or) Time Adjusted Methods (or) Present Value Methods

The pay back period and ARR methods discussed above did not recognise the time value money i.e., a rupee today is considered more valuable than the one receivable after a year or two.

Discounted cash flow methods take into account the time value of money. The basic feature of discounted cash flow methods is that they are based on discounted cash flows.

Both cash inflows and cash outflows are discounted at a predetermined discounting rate to ascertain their present values. Usually, the discounting rate is the cost of capital rate of the firm. But it can be any other rate also. Discounting factors can be obtained from present value tables.

They can also be ascertained by using the following formula:

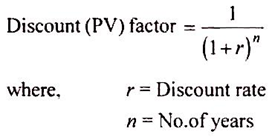
The second commendable feature of DCF methods is that they take into account all benefits and costs during the entire life of the project. Moreover, they use cash flows (i.e. CFAT) and not the accounting concept of profit (i.e., PAT).

The DCF methods are becoming increasingly popular day by day.

Following are the discounted cash flow methods :

1. Net Present Value (NPV) Method

2. Internal Rate of Return (IRR) Method

3. Profitability Index (PI)

1. Net Present Value (NPV) Method:

It is one of DCF methods in which both future cash inflows and outflows from a project are discounted at a cost of capital rate. This gives present value of cash inflows and outflows. The difference between the present value of cash inflows and outflows is called Net Present Value (NPV).

Procedure for computation of NPV

(i) Ascertain the total cash inflows of the project and the time periods in which they arise.

(ii) Calculate the present value of cash inflows i.e., CFAT _x PV factor

(iii) Ascertain the total cash outflows of the project and the time periods in which they occur.

(iv) Calculate the present value of cash outflows i.e., cash outflows x PV factor.

(v) Calculate NPV = Present value of cash inflows – Present value of cash outflows

(vi) Accept the project if NPV is positive, else reject.

If two projects are mutually exclusive, the project with higher NPV should be preferred.

Merits of NPV Method

(i) It recognises the time value of money.

(ii) It uses the discount rate which is the firm’s cost of capital.

(iii) It considers all cash flows over the entire life of the project

(iv) NPV constitutes addition to the wealth of shareholders and thus focuses on the basic objective of financial management.

(v) Since all cash flows are converted into present value (current rupees), different projects can be compared on NPV basis, thus, each project can be evaluated independent of others on its own merit.

Limitations of NPV Method

(i) This method assumes that the discount rate i.e., the firm’s cost of capital is known. But the cost of capital is difficult to understand and measure in practice.

(ii) It may not give reliable answers while dealing with alternative projects under the conditions of unequal lives of projects.

(iii) Decisions arrived at may not be satisfactory when projects being compared involve different amounts of investment.

2. Internal Rate of Return (IRR) Method

IRR is the rate of return at which the sum of discounted cash inflows equal the sum of discounted cash outflows. It is the rate at which the NPV of the investment is zero. It is called internal rate because it depends mainly on the outlay and proceeds associated with the project and not on any rate determined outside the investment.

This method is also known as marginal rate of return method or time adjusted rate of return method. This method is generally employed when cost of investment and annual cash inflows are known, while the unknown rate of return (i.e., rate of cost of capital) is to be ascertained.

Procedure for computation of IRR

IRR is calculated according to two methods on the basis of tabular values.

(a) When cash inflows are uniform for all the years:

In this case, the IRR is determined with the help of an annuity table showing the present value of Re. 1 received annually over ‘n’ years by adopting the following two steps :

Step (i) The factors to be located in the relevant annuity table is calculated by using the following simple equation:

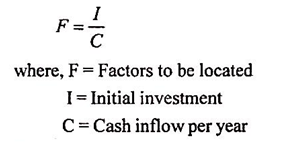
Step (ii): The factor, thus, calculated is located in an annuity table on the line representing the number of years corresponding to the estimated useful life of the assets and the relevant percentage of the discount which represents IRR.

(b) When cash inflows are not uniform:

In this case, IRR is to be ascertained by trial and error process. In this process, cash inflows are to be discounted by a number of trial rates. Just to start, the average cash inflows of different years are to be found. Original investment is to be divided by this average cash inflows. This may be taken as a present value factor.

The rate can be ascertained from PV table for this factor and at this rate, the PV of cash inflows of several years are to be calculated, then total PV of cash inflows are compared with the original investment.

If the calculated PV of cash inflows is less than the original investment, the further interpolation will be carried on at lower rate. On the other hand, a higher rate should be tried if the PV of cash inflows is higher than the original investment.

This process continues till the P V of cash inflows and the original investment are equal or nearly equal.

However, the exact rate of return can be ascertained with the help of the following formula:

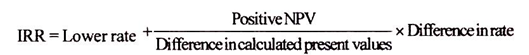
Accept or Reject criterion

Accept the project if the IRR is higher than or equal to minimum required rate of return. The minimum required rate of return is also known as cut off rate or firm’s cost of capital. While evaluating two or more projects, projects giving a higher IRR should be preferred.

Merits of IRR Method

(i) All cash inflows of the project, arising at a different points of time are considered.

(ii) Time value of money is taken into account.

(iii) Decisions are immediately taken by comparing IRR with the cost of capital.

(iv) It helps in achieving the basic objective of maximisation of shareholders wealth. All projects having IRR above the cost of capital will be automatically accepted.

Limitations of IRR Method

(i) Computation of IRR is quite tedious and it is difficult to understand.

(ii) Both NPV and IRR assume that the cash inflows can be reinvested at the discounting rate in the new projects.

However, reinvestment of funds at the cut-off rate is more appropriate than at the IRR. Hence, NPV method is more reliable than IRR for ranking two or more projects.

(iii) It may give results inconsistent with NPV method. This is especially true in case of mutually exclusive projects i.e., projects where acceptance of one would result in the rejection of the other.

Such conflict of results arise due to the following:

(a) Differences in cash outlays

(b) Unequal lives of projects

3. Profitability Index (PI) Method

This method is a variant of the NPV method. It is also known as the benefit cost ratio or present value index. It is also based on the basic concept of discounting the future cash flows and is ascertained by comparing the present value of cash inflows with the present value of cash outflows. It is calculated dividing the former by the latter.

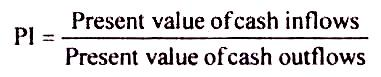
Significance of PI

The PI represents the amount obtained at the end of the project life, for every rupee invested in the project at the initial stage. The higher the PI, the better it is, since the greater is the return for every rupee of investment in the project.

Accept or Reject Criterion

Accept the project if its PI is more than 1 and reject the project if the PI is less than 1. However if the PI is equal to 1, then the firm may be indifferent because the present value of inflows is expected to be just equal to the present value of the outflows.

In case of mutually exclusive projects, the project with highest PI should be given top priority, while the project with the lowest PI should be assigned lowest priority. The projects having PI of less than 1 are likely to be outrightly rejected.

Merits of PI Method

(i) It considers the time value of money.

(ii) It is a better project evaluation technique than NPV and helps in ranking projects where NPV is positive.

(iii) It focuses on maximum return per rupee of investment and hence is useful in case of investment in divisible projects, when funds are not fully available.

Limitations of PI Method

(i) The PI as a guide in resolving capital rationing, fails where projects are indivisible. Once a single large project with high NPV is selected, the possibility of accepting several small projects which together may have higher NPV than the single project is excluded.

(ii) Situations may arise where a project with a lower PI selected may generate cash flows in such a way that another project can be taken up one or two years later, the total NPV in such case being more than the one with a project with highest PI.

The PI approach thus cannot be used indiscriminately but all types of combinations of projects will have to be worked out.

Profitability Index Vs NPV Method Vs IRR Method of Ranking of Projects

In case, a firm has two or more projects competing for the same funds at its disposal, the question of ranking the projects arises. For a given project, PI and NPV methods give the same accept and reject signals.

However, if we have to select one project out of two mutually exclusive projects, the NPV method should be preferred. It is because of the fact that the NPV indicates the economic contribution of the project in absolute terms. As such a project which gives higher economic contribution should be preferred.

As regards NPV method versus IRR method, one has to consider the basic presumption behind the two. In the case of the IRR method, the presumption is that intermediate cash inflows will be reinvested at the same rate i.e., IRR, whereas in the case of NPV method, intermediate cash inflows are presumed to be reinvested at the cut off rate.

It is obvious that re-investment of funds at the cut off rate is more possible than at the IRR which at times may be very high. Hence, the NPVs being obtained from discounting at a fixed cut off rate are more reliable in ranking two or more projects than the IRR.

Capital Budgeting – Requirements of an Ideal Method of Investment Decision Making

Given below are the requirements of a good or ideal method of investment decision making:

1. It should be based on cash-flows rather than on profits or expenditure.

2. Cash flows to be covered over the entire expected life of the asset rather than few years only.

3. It should give the absolute value of gain or loss.

4. It should consider the time value of money.

5. It should indicate relative profitability between different alternatives so that a ranking can be made between different proposals.

6. It should indicate the degree of risk and the chances of getting profit or loss in a given situation.

There is probably no method which will possess all the above attributes but different methods do possess some of them.

Stages Involved in Capital Budgeting Process

Capital investment decisions are the part of the capital budgeting process, which is concerned with determining

(a) which specific project a firm should accept,

(b) the total amount of capital expenditure which the firm should undertake, and

The following stages are involved in the capital budgeting process:

Stage # (i) Identification of investment proposals :

The capital budgeting process begins with the identification of investment proposals. The proposals may come from a rank and file worker of any department or from any line officer.

The department head collects all the investment proposals and reviews them in the light of financial and risk policies of the organisation in order to send them to the capital expenditure planning committee for consideration.

Stage # (ii) Screening the proposals:

After getting the proposals, the expenditure planning committee analyses all the proposals from various angles to ensure that these are in accordance with the corporate strategies or selection criterion of the firm and also do not lead to departmental imbalance.

Stage # (iii) Evaluation of proposals:

Evaluation of different proposals in terms of cost of capital, expected returns from alternative investment opportunities and life of the assets is the next step in the capital budgeting process.

Various methods such as pay back period, average rate of return method, NPV method, IRR method etc., are employed to evaluate the proposals.

Stage # (iv) Fixing priorities:

Once the evaluation process is over, only economic and profitable proposals are given a green signal to go ahead. But it is not possible to take up all the proposals simultaneously due to fund constraints.

In view of this, all the accepted proposals are ranked and priorities are given in the following order:

(a) current and incomplete projects are given first priority.

(b) safety projects and projects necessary to carry on the legislative requirements.

(d) projects for supplementing the income, and

(e) projects for the expansion of the product line.

Stage # (v) Final approval:

Projects finally recommended by the committee are sent to the top management along with the detailed report, both of the capital expenditure and of sources of funds to meet them. The management affirms its final seal to proposals taking in view urgency, profitability of the projects and the available financial resources.

Stage # (vi) Implementing proposals:

When the proposals are finally selected, funds are allocated for them. Such a formal plan for the allocation of funds is called a capital budget. It is the duty on the part of the top management to ensure that funds are spent in accordance with the allocation made in the capital budget.

A control over such capital expenditure is very much essential and for that purpose, a monthly report showing the amount allocated, amount spent, amount approved but not spent should be prepared and submitted to the controller.

Stage # (vii) Follow up:

Finally, a system of following up the results of completed projects should be established. Such follow up comparison of actual performance with budgeted data will ensure better forecasting and will also help in sharpening the technique of forecasting.

Steps Involved in Capital Budgeting Process

The process of capital budgeting involves generally the following steps:

(1) Project Generation:

The generation of the proposals may fall under any of the following categories:

(a) Additions to the present product line.

(b) Expand the capacity of the existing product line.

The generation of the projects may take place at the levels of top management or at the level of workers also. E.g. Proposal to replace old machine or to improve the production techniques may originate at the worker’s level also.

(2) Project Evaluation:

As in case of any types of decision makings, the capital budgeting decisions also have two faces. Firstly, estimation of the benefits and costs measured in terms of cash flows and secondly, selection of an appropriate criterion to judge the desirability of the projects.

It is necessary that the evaluation of the projects is done by impartial groups and experts in the field. Care must be taken to choose the criteria to judge the desirability of the projects and it should be consistent with the company’s basic objective to maximize the wealth.

Capital Budgeting Decisions

Criteria for Capital Budgeting Decisions:

Potentially, there is a wide array of criteria for selecting projects. Some shareholders may want the firm to select projects that will show immediate surges in cash inflow, others may want to emphasize long-term growth with little importance on short-term performance. Viewed in this way, it would be quite difficult to satisfy the differing interests of all the shareholders. Fortunately, there is a solution.

The goal of the firm is to maximize present shareholder value. This goal implies that projects should be undertaken that result in a positive net present value, that is, the present value of the expected cash inflow less the present value of the required capital expenditures.

Using Net Present Value (NPV) as a measure, capital budgeting involves selecting those projects that increase the value of the firm because they have a positive NPV. The timing and growth rate of the incoming cash flow is important only to the extent of its impact on NPV.

Using NPV as the criterion by which to select projects assumes efficient capital markets so that the firm has access to whatever capital is needed to pursue the positive NPV projects. In situations where this is not the case, there may be capital rationing and the capital budgeting process becomes more complex.

Note that it is not the responsibility of the firm to decide whether to please particular groups of shareholders who prefer longer or shorter term results. Once the firm has selected the projects to maximize its net present value, it is up to the individual shareholders to use the capital markets to borrow or lend in order to move the exact timing of their own cash inflows forward or backward.

This idea is crucial in the principal-agent relationship that exists between shareholders and corporate managers. Even though each may have their own individual preferences, the common goal is that of maximizing the present value of the corporation.

Alternative Rules for Capital Budgeting:

While net present value is the rule that always maximizes shareholder value, some firms use other criteria for their capital budgeting decisions.

Such as:

1. Internal Rate of Return (IRR)

2. Profitability Index

3. Payback Period

4. Return on Book Value

In some cases, the investment decisions resulting from the IRR and profitability index methods agree with those of NPV. Decisions made using the payback period and return on book value methods usually are suboptimal from the standpoint of maximizing shareholder value.

Features of Capital Budgeting Decisions:

1. It has the potentiality of making anticipated profits, because these decisions relate to fixed assets that represent the earning capacity of the firm. They enable the firm to generate finished goods that can ultimately be sold for profit.

2. It involves a high degree of risk. The future is uncertain and benefits from these investments are received in future years. Therefore an element of risk is involved in making these decisions.

3. Gestation period is high for these decisions, that is, the time lag between the initial investment, and expected returns.

4. These decisions have long term implications for the firm, because a failure to forecast correctly will lead to serious errors, which can be corrected only at considerable expense.

5. Capital investment is high for fixed assets, and the majority of firms have scarce capital resources.

6. Capital investment decisions once made, are not easily reversible without much financial loss to the firm, because generally, there is no market for second hand plant and machinery, and their conversion to other uses may not be financially feasible.

7. It is not often possible to estimate the costs and benefits related to a particular investment decision, because it is spread over a number of years. Similarly they are not logically comparable, because of the time value of money.

Analysis of Risk and Uncertainty under Capital Budgeting

Analysis of Risk and Uncertainty under Capital Budgeting:

The various techniques of evaluating capital budgeting projects are based on the assumption that all the projects under consideration have the same degree of risk, neither higher nor lower.

The benefits expected from a project are measured in terms of future cash inflows. Future being uncertain, actual benefits may vary from the expected benefits. Hence, there is a risk and uncertainty attached to every expected benefit.

Risk is defined as the variability or deviations from the expected return of an investment decision. The degree of risk however may differ from one decision to another decision. The value of the firm is affected by the amount of risk assumed by a firm while accepting a new project.

Hence, risk and uncertainty has to be measured and incorporated in capital budgeting decisions. This incorporation of risk and uncertainty will improve the quality of investment decisions.

Concept of Certainty, Risk and Uncertainty:

Certainty is a situation which arises when outcomes in terms of cash flows are known and determinate. For example, income from government bonds is certain and known. This is because of the sovereign guarantee attached to these bonds.

If Mr. A invests Rs. 80,000 in 5 year, 8% Government bonds then the return from these bonds @ 8% can be estimated precisely. As the return from government bonds are assumed to be certain and risk free, hence this outcome can be assigned a probability of 1. This indicates certainty of future benefits.

Risk is a situation when cash flows occurring are known with certain degree of probabilities and these probabilities are determinable. Risk situations are generally repetitive and possess a frequency distribution. But future events are not predictable with perfect knowledge.

Uncertainty is a situation where an event is not repetitive and the probabilities attached to that event are not known. In such a situation no observation can be drawn from frequency distribution.

Risk and uncertainty are used interchangeably. According to Oldster Young, “Risk refers to the set of unique outcomes for a given event which can be assigned probabilities while uncertainty refers to the outcomes of a given event which are too unsure to be assigned probabilities.”

Let us take an example of two Projects A and B. The expected cash inflows from both these projects were estimated at Rs. 30,000 each. Whereas the actual cash inflows received from projects A and B were Rs. 5,000 and Rs. 27,000 respectively. Hence, project A has proved to be more risky.

“Riskiness” of an investment project is the variability of its cash flows from those that are expected. The greater the variability, the more risky is the project. This variability may occur due to risk contributed by many factors.

The risk factors may be studied from the following view point:

(i) Standalone risk, i.e., viewing the risk of the project. This risk is project specific and may be due to change in management, strike in the company, loss due to fire/flood directly affecting the project.

(ii) Firm risk (Corporate risk), may be due to technological advancement in industry, change in industry specific rule-regulations, increase in input costs, recession in a particular industry etc. Firm risk affects the return of the firm. Because a firm takes several projects at a particular time, therefore every project does contribute to the overall risk of the firm.

(iii) Market risk affects the returns to shareholders, who are assumed to be holding diversified portfolios. This risk arises due to unanticipated changes in general economic conditions, monetary and fiscal policies, political situations in the country etc. However, expected returns from a project do also get affected due to these changes.

Portfolio Theory suggests that the consideration of market risk only will be sufficient for maximization of shareholder’s wealth. However, in actual practice this may not be fair because there exists shareholders who are not diversified and other stakeholders like lenders, Govt., suppliers, customers who are concerned about a particular project or firm i.e., about the project and the corporate risks.

Moreover, project risk, firm risk and market risks are correlated. If the economy is good and booming, the firm will flourish and if the firm does well, its projects will also do well.

Therefore, project risk can be used as a measure to know the corporate and market risk. There are various methods which are used to measure and incorporate risk in the capital budgeting projects.

Some of these methods have been discussed as follows:

1. Sensitivity Analysis:

This is also called ‘what if’ analysis. If a key input variable, such as units sold changes so will the project’s cash inflows and ultimately it’s NPV. Sensitivity analysis indicates how much a projects’ NPV will change in response to a given change in an input variable, other things remaining constant.

This analysis begins with a case situation based on expected input values. Under sensitivity analysis approach, the decision maker estimates the net present value of the project under three different circumstances i.e. pessimistic, most likely (normal) and optimistic. This helps the decision maker to have better insight of the net present value of a project.

For example, a company wants to opt for a project. There are three alternatives in the form of projects X, Y, Z under consideration.

Data relating to three projects are shown in Table 6.1 below:

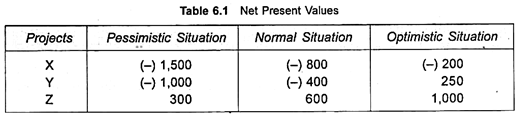
In case of X, NPV in all the three situations is negative. Therefore, this alternative is rejected.

In the case of Y, NPV is negative in two situations but positive in optimistic situations. Those who are ready to take risks may consider this project but conservative investors will not go for it.

In case of Z, NPV is positive in all the three situations. So, whether the investor is conservative or risk-taker, this project should be accepted.

Advantages:

a. It indicates the vulnerability of the project to the changes in any variable concerned.

b. It is a simple and popular technique.

Limitation:

a. In sensitivity analysis only one variable is changed at a time, whereas in practical situations many variables keep on changing at a particular point of time.

b. It is a very subjective analysis. Everything depends on the nature of the decision-maker. This analysis may lead one decision maker to accept the project while another may reject it.

2. Risk-Adjusted Discount Rate Approach:

Another way of risk adjustment is to modify the rate of return to include a risk premium wherever needed. So, greater the risk, higher should be the rate of return required from the proposal.

This is based on the premise that riskiness of the project can be taken care of, by adjusting the risk into its discount rate directly. Hence, risky projects should be discounted at a higher interest rate to take care of the risk factor.

If the project is risk-free then the discount rate may be termed as risk-free discount rate. If the project is risky then the discount rate used should be increased to incorporate the risk element of the project. This adjusted discount rate is known as Risk Adjusted Discount Rate (RADR). RADR then becomes the minimum required rate of return for the project.

This rate is then used to evaluate projects under consideration. The difference between the risky and risk-free discount rate is known as risk- premium.

Formula for RADR (k_ad) can be written as:

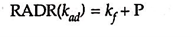
Risk adjusted discount rate can also be determined as per the following formula:

The adjustment for the risk depends on the management’s perception of the project risk and attitude of the management towards risk.

Firms generally use RADR for different investment projects. Discount rate is generally low for routine replacement investments, moderate for expansion investment and high for new projects.

Evaluation:

It is a very popular and commonly used rate. But it is very difficult to estimate this rate. It is calculated arbitrarily. This method is based on the premise that risk increases with time which is not always valid.

3. Certainty Equivalent Approach:

This approach adjusts the cash flows and not the discount rate as in RADR method. The expected future cash flows which are taken as risky are converted into certainty cash flows.

According to this method the estimated cash flows incorporating uncertainty and risk are reduced to a conservative level by applying a correction factor known as certainty equivalent coefficient (CE factor).

The CE factor can be calculated as follows:

Risk-less cash flow means the cash flow of a project which involves no risk. Risky cash flows will always be more than risk free cash flows. Hence, risky cash flows will be adjusted and these adjusted cash flows are then discounted at a risk free discount rate to find out the NPV of the project.

To summarise the above procedure, first of all, future cash flows are estimated with some degree of risk. Then CE factor is calculated. The CE factor will be different for different years. Higher the riskiness of the project, lower will be the CE factor.

Secondly, cash flows estimated are then multiplied by CE factor and certainty equivalent cash flows are found. Thirdly, these certainty equivalent cash flows are discounted at a risk free discount rate to find out the NPV of the project.

Evaluation of Certainty Equivalent Method:

This method is simple to calculate and it incorporates risk at the right place. However, it involves the subjective approach to calculate the risky or risk-less cash flows which may differ from person to person calculating these cash flows.

4. Probability Distribution Approach:

Probability means chance of occurrence of various cash flows. Probability stands for likelihood of happening in an event. If an event or cash flow has 1 probability, it means it is bound to happen and if an event has 0 probability then it will not occur at all. Probability can be objective or subjective. Objective probabilities are based on a large number of observations whereas subjective probabilities are based on personal opinion.

5. Standard Deviation:

This technique measures the variability of possible cash flows of different projects from their respective mean or expected values. A project having larger standard deviation will be more risky.

The following procedure is followed to calculate the standard deviation:

a. First of all, the mean of all the cash flows is computed.

b. Then deviation between mean and cash flows is calculated.

c. After squaring these deviations, these are multiplied by the probabilities assigned to the cash flows.

d. Finally these are totalled and their square root is calculated.

Mathematical formula for calculating standard deviation can be written as:

Coefficient of Variation:

Coefficient of variation is calculated where the projects have different outlays or have different mean values. In this case coefficient of variation would be –

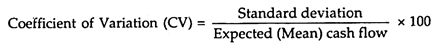
6. Decision Tree Analysis:

This method to analyse risk is a formal diagrammatic display of various decision alternatives followed by chance events which may occur with some probability. It’s a graphical presentation of a sequence of possible outcomes with a schematic representation of the problem.

The computations and results are shown in tree-form so that the information can easily be understood. Sequences of events is shown like the branches of a tree, cash flows of year 1 are related to the cash flows of year 2.

Many capital budgeting decisions are not made at a single point of time. They consist of two or more sequential decisions. The cash flows expected under each alternative are multiplied by the probabilities of occurrence of the events.

Capital Budgeting Situations

In real life situations capital budgeting decisions are complex. Financial Manager may face some situations when he has to adopt a separate procedure for evaluating investment proposals.

Some of these situations are:

1. Replacement situations.

2. Projects with unequal lives.

3. Capital Rationing.

1. Replacement Decisions and their Relevant Cash Flows:

The replacement decision is one of the important capital budgeting decisions taken by firms from time to time. Under a replacement decision, the existing machine is replaced with a new machine. The need for replacement of old machines arises because of many reasons i.e., to increase production, to reduce cost, to improve the quality of the product etc.

For evaluating replacement decisions in capital budgeting, an important assumption is that the useful life of the new asset is equal to the remaining useful life of the existing asset being replaced. For example, if any existing machine is having its useful life of 5 years then it is assumed that a new machine proposed to be installed to replace the existing one will also have a useful life of 5 years.

This will help in easy comparison of cost and benefits of both However if the assumption of equal life period is relaxed then these proposals will become “proposals with unequal lives.”

The calculations of relevant cash flows for replacement decisions with an assumption of equal lives of new and existing machines are different. To determine cash flows for replacement decisions an incremental cash flow approach has to be adopted.

After comparing the cash flows of both new and old assets, the difference in revenue and costs of both are calculated. Incremental income before and after tax are calculated. Finally incremental cash flow of the replacement project is calculated.

This is shown as follows:

2. Projects with Unequal Lives:

The contradiction in results given by NPV and IRR method for two mutually exclusive proposals having unequal lives can be resolved by adopting altogether different procedures. It would be wrong if we base our decision on NPV methods for proposals having different lives. This is because of the different reinvestment rates assumption.

To resolve the problem, the project with a shorter period may be assumed to be replaced on its termination on the terms of producing the same cash flows of similar pattern in future. In this situation the cost and benefits of such proposals can be measured on some common basis. This common basis may be either to compare the results over equal length of time or to find the benefits on an annualised basis. Accordingly two methods can be discussed to resolve the problem.

These are:

(i) Common time duration method.

(ii) Equivalent Annual Value (EAV) method.

(i) Common Time Duration Method:

Under the common time duration method, the cost and benefits of two mutually exclusive proposals are measured for equal duration of time and then compared with, to arrive at a decision. A project with a shorter duration is assumed to be automatically replaced on its termination on the terms of same cost and benefits (cash flows).

This method however suffers from many shortcomings. One of the shortcomings is because of its assumption of the same cost and benefits in terms of cash flows of the short lived projects on their replacement. This may not be true because of inflation and availability of different investment opportunities at different points of time.

(ii) Equivalent Annual Value (EAV) Method:

Another method to compare the benefits of two mutually exclusive projects with unequal lives is to find the equivalent annual value (EAV) of the proposals under consideration. The equivalent annual value so calculated will form the basis for acceptance/rejection of the proposals.

The equivalent annual value can be calculated by adopting the following formula:

(a) For Revenue Addition Projects:

EAV for revenue addition projects can be calculated by dividing NPV of a proposal with the PV annuity factor at the given discount rate for the life period of the project.

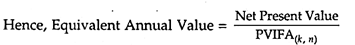
Where, PVIFA = Present value interest factor for annuity at discount rate (k) for n years.

Since the objective is to maximize the EAV therefore, a proposal having higher EAV is recommended for adoption.

(b) For Cost Reduction Projects:

For cost reduction projects having equal capacities, equivalent annual cost can be calculated for decision making. Equivalent annual cost can be calculated by dividing the present values of all cash outflows with the PV annuity factor at the given discount rate for the life period of the proposal.

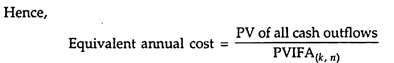
Since the objective is to minimize the equivalent annual cost, therefore a proposal having less equivalent annual cost is suggested for implementation.

Risk Analysis in Capital Budgeting

Risk analysis in capital budgeting is summarised below:

Our analysis of capital budgeting decision making was so far based on the assumption that whatever estimation of cash flows has been done which will hold certain. This, however, is not correct.

In spite of the best techniques that may be adopted for estimating cash flows, it is not possible to ensure that the actual cash flows turn out to be exactly, what they were estimated to be. Every project is a future oriented activity and, therefore, uncertainty cannot be avoided, in spite of best efforts on our part.

The uncertainty may be on account of both internal and external conditions. The external conditions are – changes in market conditions, introduction of another product by a competitor, import liberalization, change of tastes and fashions, tax policies etc.

The internal conditions are breakdown of machinery, labour turnover, internal managerial problems etc. These uncertainties may eventually result in a profitable project to be a loss making one and if this happens, the whole objective of project appraisal is defeated.

How to Overcome this Problem?

Since uncertainty cannot be exactly estimated, we discuss here some methods to create safeguards and reduce the risk in our decision making.

1. Conservative Estimates:

The simplest method is to use conservative estimates. Since initial outflows are fairly certain, the real problem is in estimating future inflows. Here the strategy is to take conservative estimates and make calculations accordingly.

For example, in a project, the three persons assigned with making estimates, make following estimates of inflows:

In a normal course, we take a mean of Rs.15000 and then make our calculations accordingly. While making a conservative estimate, we will take a figure of Rs.14000 only. In this way, we will make conservative estimates for each year and then on the basis of these estimates calculate NPV, IRR, PI, Payback etc.

The NPV so calculated will automatically have a safety margin. Some small variations from a normal (mean) situation will not jeopardize our project and it will continue to be profitable.

2. Certainty Equivalent Coefficient:

Another method to create a safety margin or a cushion is called the certainty equivalent coefficient (CEC) which, when multiplied by the given cash flows, gives a certain cash flow. For example, if the estimated cash flows are Rs. 10,000 and the certainty equivalent coefficient is .8, then this Rs. 10,000 worth of cash flow should be treated equivalent to Rs. 8,000 only.

The advantage of a certainty equivalent coefficient is that it can be made a scaled one also, e.g., based on time. A cash flow in period 1 may be given a CEC of .95 and a cash flow in period 2 may be giving a CEC of 0.9 and so on. This will automatically ensure that cash flows in later years have a lower weightage, than the cash flows of earlier years.

Illustration:

A company wishes to make an investment of Rs. 1,00,000 for a 5 year project.

The cash flows and certainty equivalent coefficients for different years are as follows:

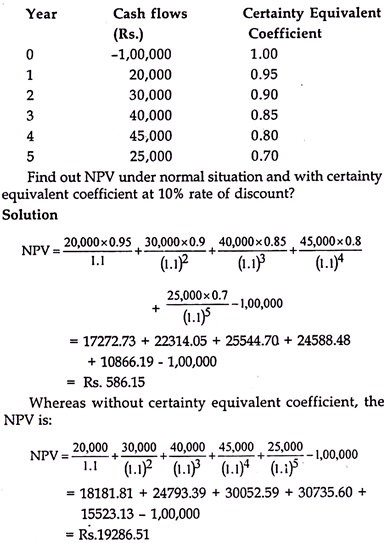
Thus, we find that a project when calculated without considering risk gives a positive NPV. But its NPV falls drastically, once we incorporate risk into its cash flow estimates. It is better to keep away from such risky projects.

The problem with the above method is that there is no scientific method for calculating certainty equivalent coefficient and it is largely the subjective judgment of a person responsible for making such estimation. Using this method is, therefore, fraught with problems.

3. Risk-Adjusted Discount Rate:

In order to create a cushion in our capital budgeting decision, we may use a discount rate which has been adjusted for the riskiness of the project. If a project is risky, we use a higher interest rate to discount our cash flows. The reason behind this approach is that a more risky investment should have a higher required rate of return and this is logically consistent with the shareholders objective of maximizing the returns.

Since the investors are inherently risk averse, the risky project should carry a higher required rate as a risk premium. The greater the degree of risk, the greater will be the required rate or the discount rate.

The relationship between the risk and the required rate/ risk adjusted discount rate has been shown in the following figure:

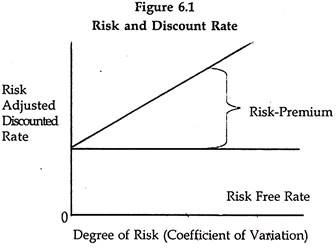
The accept-reject rule in case of risk adjusted discount rate is dependent upon which method we use. If we are calculating NPV, then the simple rule is that if NPV calculated at the risk-adjusted discount rate is positive, the project is acceptable.

If we are using IRR, then the acceptance rule is that IRR should be greater than risk adjusted discount rate otherwise the proposal should be rejected. In the illustration given above (under certainty equivalent approach) the NPV at risk free rate (10%) is Rs. 19286.51. Suppose the risk premium is 2% and therefore the risk adjusted discount rate would be 12%.

At this rate the NPV value will be:

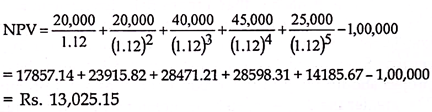
If the risk is greater, a higher discount rate should be used and even after this higher rate if the NPV is positive, then the project should be accepted.

The Capital Asset Pricing Model (CAPM) is a scientific method to calculate the risk premium and the risk adjusted discount rate. Although it was initially developed for portfolio analysis, it can be applied to capital budgeting decision making also.

Under the CAPM the risk adjusted discount rate is found as under:

In using all these methods, it should be ensured that only one of the above methods should be used. For example, if we are using conservative estimates, we should not use the certainty equivalent coefficient or the risk adjusted discount rate.

Similarly, in using a certainty equivalent approach, neither the conservative estimates be used nor the risk adjusted discount rate should be applied. We should use only the risk free rate of discount in making our calculations. If more than one method is used simultaneously; it will lead to double counting of risk and will lead to wrong conclusions.

So far we have analysed simple methods to tackle risks. Although these methods are fairly useful, they lack scientific approach and accuracy. It is, therefore, necessary that we use more scientific techniques, which can help us make a correct decision under a variety of conditions.

4. Probability Distribution Analysis:

When we are estimating cash flows for the future, we assume a sort of a normal situation and then make our estimates accordingly. However, a normal situation is not likely to always prevail and things may be more favorable or less favorable to a company. A more favorable situation would mean that future cash flows are higher than expected and an unfavorable situation would mean that cash flows are lower than estimated.

This can be further analysed as a highly favorable or highly unfavorable scenario. After, identifying these favorable or unfavorable including highly favorable or unfavorable scenarios, the next step is to assign probability to each scenario. The normal situation should have the highest probability, implying that this is the most likely situation and favorable and unfavorable scenarios should have lower probabilities.

A likely five scenario probability distribution along with estimated cash flows may be presented as follows:

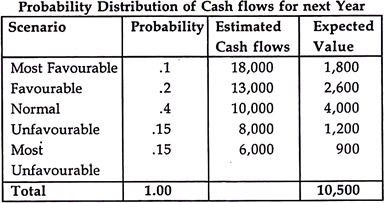
The above table implies that, as per our estimates, 40% chances are that situation will be normal and would yield a cash flow of Rs. 10,000; 20% chances are that things would be favorable to us, which would give us a cash flow of Rs. 13,000 and 10% chances are that things would be highly favorable and if it is so we will get cash flows of Rs. 18,000.

On the negative side, 15% chances are of unfavorable and most unfavorable situations which are likely to yield cash flows of Rs. 8,000 and 6,000 respectively. In this way all the possibilities are covered and that is why the sum of all the probabilities is equal to 1.0.

After getting these five cash flows with five probabilities, the next step is to find the mean value or called the ‘expected value of the probability distribution.’ This is found by multiplying each cash flow by the respective probability and then taking a sum of these values.

In the above case, we see that the expected value of the entire probability distribution comes to Rs. 10,500. Thus we see that although the expected cash flow of the normal situation is Rs. 10,000, the sum of all the probabilities shows that the expected value of the entire scenarios is Rs. 10,500. In this way, expected values for different years of a project life may be calculated.

After calculating the expected values of cash flows for different years, we can find the Net Present Value (NPV) of a project in the same way as we have done earlier.

The formula for the same would be:

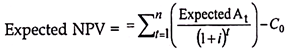
The rate of interest shall be the risk free rate of interest.

However, the expected NPV of the project would not serve any purpose unless we are also able to measure the risk involved. The expected value may be high but if the risk involved is also high, then we must exercise due caution in our decision making. The problem, therefore, is how to measure the risk?

Risk Measurement:

Risk is the degree of uncertainty of a given outcome. If the probability of a given outcome being away from the expected value is high, we call it a higher risk. If the probability of a given outcome is very close to the expected value, the risk is very low.

This can be explained by the following examples:

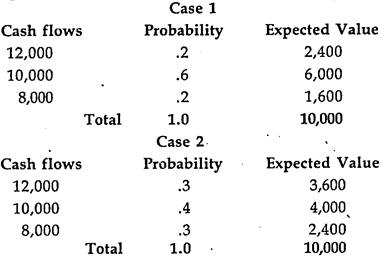
In the above example, in case 1 and in case 2, the expected value is the same but we see that variability of outcomes is different. In case 1, 60% chance is that cash flows will be 10,000 and only 20% chances are that cash flows would be 12,000 or 8,000. In case 2, the chances of cash flows being 10,000 is only 40% and 30% chances are that cash flow would be 12,000 or 8,000 respectively. Thus, the degree of certainty is much higher in case 1 and variability is much higher in case 2.

This variability of an outcome is measurable through the statistical measure of ‘Standard Deviation’ (SD or ‘σ’). This SD measures the variability of a given distribution around the mean value. Hence, in order to measure the risk in a given project, we need to find the standard deviation of the expected NPV.

For this purpose, we need to find the standard deviation of cash flows for each year and then we calculate the combined SD of all the years together, which gives us the variability of the NPV of the project as a whole.

We can explain this by way of an illustration. For the purpose of simplicity, we take the project life of three years and for each year we take three scenario probability distribution.

Illustration:

A company is planning an investment of Rs. 5,000 in a project which has a useful life of 3 years. The company’s finance and marketing department has made 3 scenario projections of cash flow after tax for 3 years. The discount rate is 10% per annum. Find the NPV of the project and its standard deviation.

How shall we interpret the value of standard deviation?

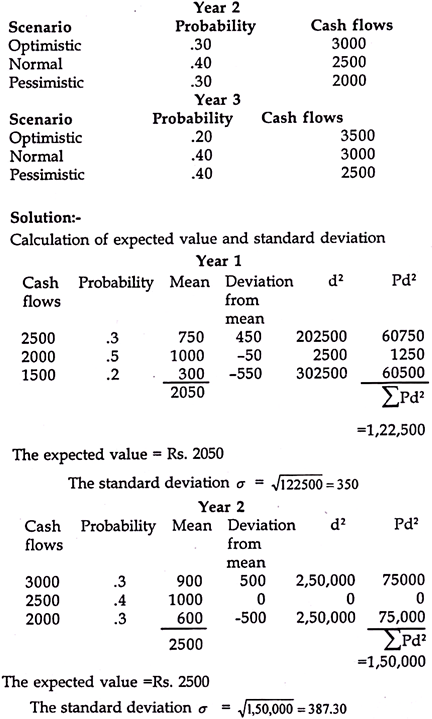
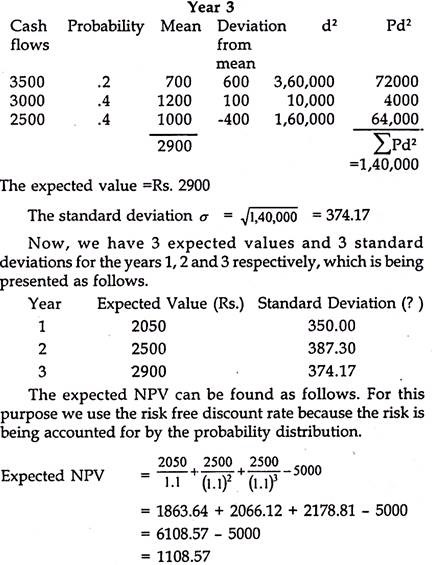
Now we have to find the combined standard deviation. The combined standard deviation for 3 years depends upon the relationship between the cash flows of different years. It means to what extend the cash flow of year 2 depends upon the cash flow of year 1 and to what extent the cash flows of year 3 depend upon the cash flows of year 2 and so on

In this connection 3 situations can be visualized:

a. Independence of cash flows i.e. cash flows of different years has no relation with each other. They happen independently (randomly).

b. Perfect relationship of cash flows, i.e. cash flows of each year depends upon what had happened in its previous year.

c. Moderate relationships in cash flows i.e. the cash flows of year 2 are neither perfectly independent nor are they perfectly correlated, but they are influenced by the cash flows of the previous year. In other words, the cash flows of year 2 are likely to be high if the cash flows of year 1 have been high and are likely to be low if they have been low in the previous year and so on.

The combined standard deviation depends upon the nature of this relationship between cash flows of different years. Let us take them up one by one.

a. Independence of cash flows:

If cash flows of different years are independent, the combined standard Deviation is:

b. Perfectly Correlated Cash Flows:

If cash flows of different years are perfectly correlated, the combined standard deviation is:

c. Moderately Correlated Cash flows:

If cash flows are moderately correlated, the combined standard deviation may be determined as follows:

When we calculate the combined standard deviation we find that each year there are 3 possibilities and so the number of series will be 3x3x3 = 27.

We now see how the series are found:

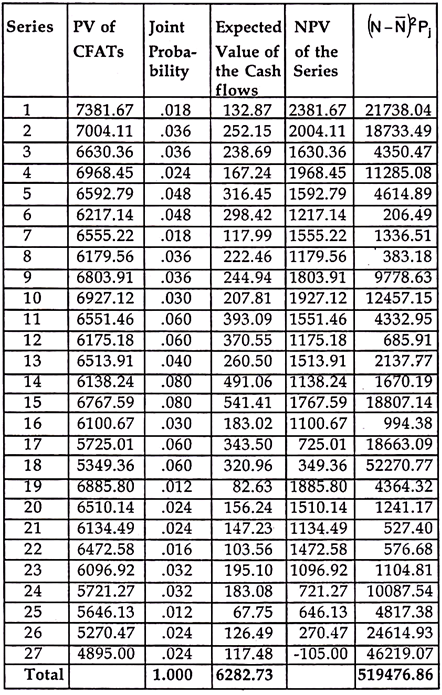
The first row is the first possibility for each year with cash flows of 2500, 3000 and 3500 for the three years respectively.

We then discount them as follows to find the present value of cash flow:

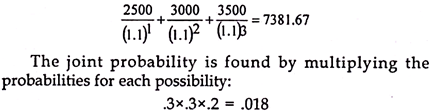
We then multiply the present value of the cash flows with the joint probability to find the expected value of the series 1. The sum of all these expected values gives the total expected value of 6282.73. We subtract the initial outflow of 5000 to find the total expected value of the project which is 1282.73. In the fifth column we find the NPV of the series by subtracting the amount of 5000 from the present value of the series which is 7381.67 to get the NPV of the series at 2381.67.

The last column is found as follows:

The standard deviation is an absolute measure of variability of any given distribution and is, therefore, not suitable to compare the variability of two distributions when their mean values are different. In order to make this comparison between the risks of two distributions, a relative measure of variability is to be used, which is called the coefficient of variation which is found as follows –

Thus, we find that minimum risk lies when cash flows are independent and maximum risk lies when cash flows are perfectly correlated. The risk in case of moderately correlated cash flows is also moderate.

Interpretation of Standard Deviation:

The expected NPV and the Standard Deviation provide us with useful information about the possibility of obtaining the NPV between any two given values or obtaining NPV above a particular value and so on.

For this purpose, we assume that over a period of time, the probability distribution corresponds to a ‘Normal Distribution’. The normal distribution has some specific peculiarities and we make use of these peculiarities to derive the information that we need.

The ‘normal distribution’ is shaped as follows:

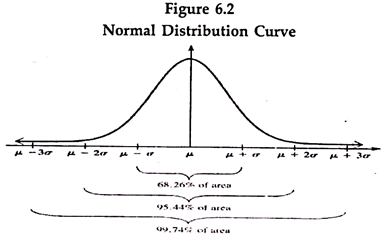
In a normal distribution 1 σ from the mean value each side covers 34.23% of the area. So the total area covered between l σ ± of the mean value is 68.46%. Similarly, 2 σ each side covers 47.72% of the area. In other words, the area covered between 2 σ ± of the mean value is 95.44%. Other values can be found by looking at the Normal Probability Distribution table or the ‘Z’ table.

Another way to look at the ‘Z’ table is to measure the value of one tail or the area covered under one tail. For example, one side of the mean line has 50 percent of the area. One standard deviation on one side covers 34.23 percent of the area. Therefore, the area of the tail will be 50 – 34.23 = 15.77 percent. Similarly, the area covered under two standard deviations from the mean value on one side is 47.72 percent.

Hence, the area covered under the tail for two standard deviations from mean is 50 – 47.72 = 2.28 percent. Similarly areas under different values of standard deviation from the mean value for a tail can be calculated. Both variants of the Normal Probability Distribution Tables are available. The user should, therefore, be cautious in using the Normal Probability Distribution Table.

The use of this normal distribution table can be explained by a simple example. Suppose, the mean NPV or the expected value of the NPV is Rs. 500 and the standard deviation is 200. In this case it implies that 68.46 percent of the chance is that the actual NPV will be between 500-200 = 300 and 500+200 =700. Further, 95.44 percent chance is that the actual NPV will be between 500 ± 2 σ or between Rs. 100 and Rs. 900. In this manner, chances of having a given value can be found.

For example, if we want to find out the probability that the project does not suffer a loss, we have to find the value of the standard deviation from the mean which satisfies our condition. In this case the value of zero profit is 2.5 σ from the mean.

This is also the value of one tail. The value of one tail at 2.5 σ according to the ‘Z’ table is .0062. This implies that there is only .62 percent chance that the profits would be less than zero or there is an actual loss. The rest of the probability i.e. 99.38 percent is that we will get a profit.

Now, we would like to apply this principle to the illustration that we have solved earlier. We have seen that the NPV is 1108.57 while the standard deviation is 531.71, if the cash flows are assumed as independent. It implies that 68.46 percent of the chance is that the actual NPV will be between 1108.57 + 531.71 = 1640.28 and 1108.57 – 531.71 = 576.86.

If, however, the cash flows are perfectly correlated, then 68.46 percent of the chance is that the actual NPV will be between 1108.57 + 919.38 = 2027.95 and 1108.57 – 919.38 = 189.19. We do find that the probability of getting a loss increases if the cash flows are perfectly correlated.

This information can be further utilized to find the probability that it will not end up in a loss. In other words, it does get some profit. For this purpose, we calculate the value in terms of standard deviation.

If the cash flows are independent this value is:

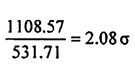
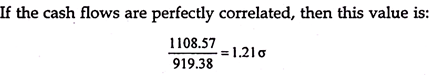
The tail value of 2.1 σ is 0.0179 and of 1.2 is .1151. This can be interpreted to mean that if the cash flows are independent then the probability of getting a loss is only 1.79 percent but if the cash flows are perfectly correlated then there are 11.51 percent chances of getting a loss. Thus, the degree of safety of a project can be reasonably assessed.

Thus, we find that the measurement of standard deviation and the use of ‘Z’ table is a very useful methodology to assess the variability of cash flows and for measuring the degree of safety of a project.

More than One Project:

Another problem in connection with the risk analysis in project appraisal is to find out the combined NPV and the standard deviation if more than one project is being evaluated. As far as finding the combined NPV is concerned, it is the sum of individual NPVs of two projects.

For finding the combined standard deviation of two projects, say ‘x’ and ‘y’, we use the following formula:

Illustration:

A company is considering the implementation of a project ‘x’ for which the NPV is Rs.8,000 and the standard deviation is 3,500. While the company is considering the implementation of this project, a proposal for an additional project ‘y’ is made for which the NPV is expected to be Rs. 6,000 and the standard deviation is expected to be 2,500.

The coefficient of correlation between the two projects is estimated as .75. Calculate the combined NPV of the two projects and also find out whether the riskiness of the projects increases if the second project is also undertaken by the company?

Solution:

5. Sensitivity Analysis:

Another method to deal with risk and uncertainty in project appraisal is the sensitivity analysis. A project’s appraisal is done on the basis of certain assumptions about different variables which might not hold well in future. Any change in these variables may threaten the profitability of the project and would make our decision making wrong.

In order to prevent the happening of this eventuality, a ‘sensitivity analysis’ may be done in advance. The sensitivity analysis tells us the impact of change in any of the given variables on the given outcome. In short, it measures the sensitivity of an outcome to the changes in given variables.

These variables may be classified in three broad categories:

(i) Those which impact the cash outflows. These may be change in machinery or equipment cost, transportation cost, installation cost, operating expenses, cost of raw material, wages, taxes and other expenses.

(ii) Those which impact the cash inflows. These may be the price of the product, output to be produced, subsidies or grants which may be received etc.

(iii) Those which impact the discount rate. The changes in the rate of interest charged by the lending institutions, administrative expenses, floatation expenses, tax rates etc. may bring about a change in the discount rate.

Any increase in cash outflows will reduce the NPV of a project and may make a profitable project into an unprofitable one. Similarly, any reduction in the price of our product or any disruption in production will also seriously reduce the cash inflows over the life of the project.

The change in the interest rates, tax rates and other costs related to raising of loan or equity will impact the cost of capital and the discount rate and may seriously impact the profitability of the project. Sensitivity analysis is the process of assessing the impact of these changes on the payback, NPV or the IRR of the project. In order to illustrate it, we take the following illustration.

Illustration:

A company is planning an investment of Rs. 1,00,000 in a machinery which has a useful life of 5 years. The machinery is expected to produce toys. The number of units of toys, the price and cost of production is expected to be as follows. The rate for discount is 15 percent before tax and the tax rate is 40 percent.

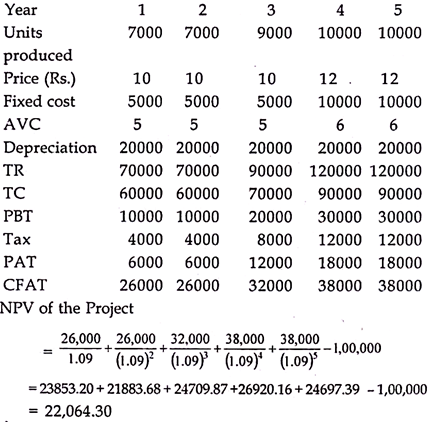
This is the NPV of the project as per the given assumptions. Now we can test the sensitivity of this project with respect to various changes in the independent variables.

(i) Change in Tax Rate:

We have taken the before tax cost of capital at 15 percent. With a tax rate of 40 percent, the after tax rate is 9 percent. Suppose, the tax rate increases to 50 percent. In this case the after tax rate of discount becomes 7.5 percent.

With this discount rate the NPV of the project changes as follows:

In this way we find that the NPV of the project decreases if tax rate increases from 40 percent to 50 percent.

(ii) Change in Fixed Cost:

Suppose the company is required to incur an additional fixed cost of Rs. 3000 p.a.

The CFATs would then become:

Thus, we find that if fixed cost increases by Rs. 3000 per annum, the NPV of the project decreases from Rs. 22,064.30 to 10,396.24

(iii) Increase in variable cost by Re. 1 per unit:

If the AVC increases by Re. 1 then the CFATs would be:

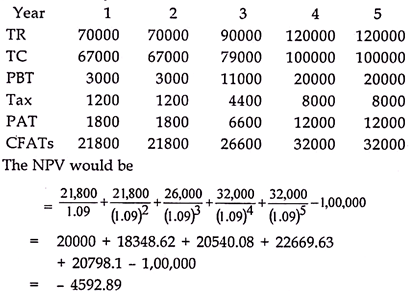
Thus, we find that the NPV is very sensitive to the changes in cost. Even a Re. 1 increase in average variable cost makes the project unviable. Thus, sensitivity of NPV to different values of average variable cost can be tested.

Now, with increasing computerization the sensitivity analysis can be done very conveniently. With the click of a button, sensitivity of Payback, NPV or IRR of a project can be tested with reference to different values of a given variable or a combination of variables.

Sensitivity Analysis is used as a tool to assess the riskiness of a project. It gives us a fairly good idea of the impact of a change in output, price, cost, interest rate, tax rate etc. and helps us assess the viability and riskiness of a project.

6. Scenario Analysis:

Sensitivity Analysis evaluates the impact of change in a given variable on any of the decision tools – Payback, NPV or IRR. However, Scenario Analysis may make a more comprehensive analysis of drawing up different scenarios where several variables are changing at the same time.

For example, we may have two scenarios in the above example, with different variables as follows:

Now on the basis of these variables, NPVs can be calculated for each scenario. This gives us a good idea of how NPV or IRR are changing when several variables are expected to change in a given direction and this helps us estimate our risk and take an appropriate decision.

Capital Budgeting – Investment Decision

Investment decision is referred to the activity of deciding the pattern of investment. It covers both short term as well as long term investment, in other words fixed assets and the current assets.

Long term investment decision is about the allocation of capital to investment projects whose benefits accrue in the long run, short term investment decision is about allocation of funds as among cash and receivables and inventory etc.

The funds invested in assets should also yield maximum return to the business concern. Hence, it is a risky decision where the finance manager has to take maximum care in selecting the areas of investment. As the future is uncertain the returns expected must cover both risk as well as the uncertainties.

The selection of proposals can be evaluated by using certain techniques like costing technique, capital budgeting, CVP analysis etc., before making final decisions on the investment avenues.

Factors

The factors considered while making capital investment decisions are:

(i) Large Investments:

Capital budgeting decisions generally involve large investment of funds. But the funds available with the firm are always limited and the demand for excess is necessary to purchase the resources.

(ii) Long Term Commitment of Funds:

Capital investment involves not only the large amount of funds but also funds for long term or more or less on a permanent basis.

(iii) Reversible Nature:

The capital investment decisions are of reversible nature. Once the decisions are taken, these decisions can be changed according to the market situations.

(iv) Long Term Effect on Profitability:

Capital investment decisions have a long term and significant effect on the profitability of a concern. Not only the present earnings of the firm are affected by the investment in capital assets but also the future growth and profitability of the firm depends upon the investment decision taken today.

Capital Budgeting – Capital Rationing

A finance manager can manage to raise resources to finance all projects promising higher yield in relation to their cost. However, in the real world, we find that there is constraint to the supply of capital particularly from external sources.

In view of the availability of limited amounts of capital a firm usually sets an absolute limit on the size capital budget for one year. Such a state of affairs is designated as capital rationing.

In such a situation, the finance manager will not be able to accept all projects yielding positive net present values. This policy, therefore, tends to restrict the ability of the firm to reach the profit maximization goal. Within the overall limit a finance manager has to select such a combination of projects as maximize profit.

The following example will illustrate how projects are ranked under capital rationing scheme:

Illustration:

Good Luck Company has set a limit of Rs.8,00,000.

The company has the following projects in hand, having been ranked in descending order of profitability indexes:

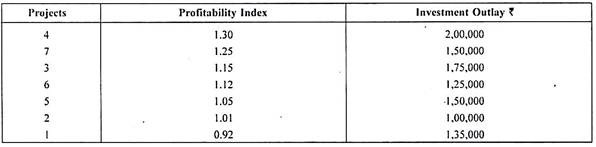
Which projects should be selected by the company under the capital rationing scheme so as to maximize its value?

Solution:

Under the scheme of capital rationing, the management should accept projects arranged in descending order of their profitability so long as the budget is exhausted. With a capital limit of Rs.8,00,000 only five projects (project 4.7, 3, 6 and 5) could be selected for implementation. Project 2 with higher yield than the cost could not accept because of budget constraint.

Another important feature of project selection under the capital rationing scheme is that the firm should accept several smaller but less profitable projects to allow fuller utilization of the capital budget instead of accepting one large project with relatively higher yield that leaves a portion of the budget unutilized. This course of action will help the firm to maximize profitability.

Appraisal of Capital Budgeting Proposals

The financial executive evaluates the proposals of capital expenditure. Such proposals may originate in production, distribution, research or any other department. Any method of appraisal of capital investments plays a vital role in maintaining or increasing the profitability of a business.

In evaluating the feasibility of a long-lived capital project, the uncertainties inherent should be assessed. When the capital available is limited, it is essential to establish a system of priorities so that the best use is made of it.

Such a list of priorities may be the one given below:

(i) Projects already in hand;

(ii) Projects necessitated by law;

(iii) Projects to maintain capacity;

(iv) Projects to increase earnings;

(v) Projects to develop new products.

The evaluation of an investment calls for an identification of alternatives, feasibility studies and pragmatic cash flow forecasts, appraisal of economic worth vis-a-vis the risks involved and the expected rate of return, pilot studies, approach plan, prototype testing, sanction from competent authority, follow-up and post-audit.

Despite the more sophisticated approaches possible through probabilistic techniques to allow for risk and uncertainty, the discounted cash flow return and the net present value techniques are helpful in most common situations. A number of methods have been used in formulating project acceptability standards.

In the past, some highly subjective and judgemental approaches were used and tolerated. Project evaluation is future- oriented and invariably contains some element of subjective judgement, even a measure of intuition. But the current emphasis is on the objective-quantified approaches which concentrate on a comparison of project cash flows.

In this connection, P. Chandra observes that in a discussion of investment analysis, the principal focus is generally on the criteria of investment appraisal. The measurement of costs and benefits is often affected in a low key.

From the practical angle, however, this is very important. Harold Bierman and Seymour Smidt suggest a manual for analysing investment decisions. The manual focuses attention on the quantitative aspects of an investment decision; it also allows for the presentation of descriptive material which gives the pros and cons of different investment opportunities.

The manual gives the following explanations:

(i) Description and Justification Summary

This is a brief statement of the nature of the project and the type of benefits expected.

(ii) Risk Analysis Summary

It describes uncertain events of different types, depending upon how they affect the cash flow of a project.

(iii) Cash Flow Summary

More than one cash flow estimates are prepared; and each indicates the expected outcome.

(iv) Summary of Economic Measures

The summary includes the most probably present value, the probable yield, the cash payback period and the effect on income in the short run as well as in the long run.

(v) Probability of a Loss

The probability of net present value being less than zero is calculated.

Methods of Appraising Capital Budgeting Proposals:

Practical Methods:

Firms required to commit funds over a long period of time prefer the recoupment or payback method for discounting the risks. The long-period method gives the firm a long or finite horizon, and the method is known as the finite planning horizon method.

Another practical method, known as the risk discounting method, combines the reduction of an expected flow, both for risks present and for the future. The projects are first ranked on the basis of the estimates of their net cash flows.

Thus futurity is taken care of; but the degree of risk involved in these projects is ignored. To consider this risk, cash inflows are discounted at different rates for different projects. A riskier project is discounted at a higher rate. The difference between the cost of capital and the discount rate is referred to as the risk factor.

Another approach to the risk discounting method is to directly discount estimated future flows to different periods, and subsequently adjust these amounts on the basis of a finite horizon method.

The third practical method, known as the sensitivity analysis tests the robustness of a given proposal. The term applies to all formulations under the generic name mathematical programming. It offers different solutions to the problems and suggests implications of possible errors in the original problem formulation.

Difficulties

While evaluating the capital budgeting proposals, a finance manager has to undergo many difficulties like:

1. Risk and Uncertainty:

Capital budgeting proposals relate to the long-term future period which is uncertain. Although a finance manager forecasts the cash flows based on estimates of future costs, revenue, demand, external environment etc. to the best of his knowledge and analytical skills, even then accurate forecasts cannot be made.

Hence an amount of risk and uncertainty is always attached to capital budgeting decisions. The risk and uncertainty may be in terms of estimated cash outflows and inflows, estimated rate of return, future economic and political situations etc.

2. Time-Element:

Different timings and patterns of cost and benefits of an investment proposal is an important problem area in capital budgeting. Most of the capital budgeting decisions involve investment of funds at zero periods. The benefits of the investment proposal will occur over a longer period in future.

Hence the cost and benefits of a long-term investment decision occurs at different points of time. Cost and benefits occurring at different periods are not comparable until and unless adjusted for their time value of money. Therefore these have to be made comparable by either adopting compounding or discounting techniques.

3. Difficult to Measure:

Measuring the cost and benefits of a project in quantitative terms is very difficult. Capital budgeting decisions are based on the estimated future cash inflows of a proposed cash outlay.

These future cash inflows are further based on certain assumptions of cost and revenue. For several reasons, the cost and revenue realised may not be in line with the estimated one. Further an investment proposal may have side effects.

For example when a new product is launched, the question may arise whether the launch of a new product will increase or decrease the sale of a firm’s existing products. If yes, then how much and what will be its impact on the overall profitability of the firm?

These questions are difficult to answer because of difficulty in measuring these side effects. Hence measuring the cost and benefits of a proposal is another problem in capital budgeting.

4. Capital Rationing:

Capital rationing is also one of the important problems in capital budgeting. Capital Rationing is a situation when a firm has many projects to be undertaken but has limited funds to spend or when there is some ceiling on the availability of funds.

In such a situation different projects have to be ranked according to an evaluation technique and then projects are selected accordingly. Ranking the various projects and allocation of scarce funds among them is again a difficult job undertaken by the finance manager.

Conceptual Methods:

The conceptual methods include the shackle approach. G. S. L. Shackle suggests that the problems of risk and uncertainty can be handled by focusing on the mental and psychological processes involved in investment decisions. He argues that decision-makers expect two extreme outcomes to a proposal.

One is the representative potential gain called focus gain. The other is a representative potential loss called the focus loss. He discards the notion of risk discounting in favour of a concept called potential surprise, which follows unexpected outcomes. The occurrence of an outcome with low probability contains a high element of surprise and vice-versa.

He applies the concepts of information theory to business decisions, and relies on subjective probability. He believes that decisions involving a number of mutually exclusive investment opportunities are essentially subjective.

Probabilistic Methods:

There are two techniques which employ the probabilistic methods for an analysis of investment decisions:

(a) Frederick S. Hillier utilises analytic techniques. He argues that it is necessary to develop the probability distribution of the present value of an investment proposal. This will enable a firm to derive the expected value and variance of the net present value of a single project. He attaches great importance to the hypothetical probability density function.

(b) David B. Hertz employs simulation techniques. His model is a three-stage simulation. The management estimates the range of value of each relevant independent variable. Each value is associated with the likelihood of its occurrence.

The variables include sales, range of selling prices, inventories, present and future outlays, etc. In the next stage, the management uses standard statistical sampling techniques to select a specific value for each variable, combine all the values and compute the rate of return or some other criterion.

Each combination is technically called iteration. There are a pre-specified number of iterations to define and evaluate the probabilities of occurrence for each possible rate of return or some other criterion. The average expected rate of return is computed from the weighted outcomes.

When the average expected return and the variability for each proposal have been estimated, the management decides to accept or reject a proposal. Hertz utilises nine input variables belonging to three classes-market analysis, investment-cost analysis and operating and fixed cost analysis.

The effectiveness of an appraisal system depends upon its ability to take a range of competing investment proposals and assess them against two requirements-

(i) to provide a selection of projects by ranking them in order of profitability and

(ii) to ensure that investments are not made in projects which earn less than the cost of capital, or the appropriate minimum or cutoff rate of return.

An appraisal system not performing both these functions adequately makes at best only a limited contribution to the management process. At the worst, it leads to wrong decisions.

Administrative Methods:

Capital budgeting decisions involve a lot of administrative procedures. Usually, approvals are required at higher levels of management within the organisation. In most businesses, line managers originate investment proposals, and if the Board of Directors merely allocates funds in the order of profitability, investment decisions (disposition of funds) may not be in accordance with corporate strategy.

The horizon of line managers tends to be generally restricted; and they may not be fully informed about corporate strategy. Moreover, their immediate aim may be short-term and not forward-looking, and their judgement may be impaired by this fact.

In addition since capital budgeting is not an exact science, approximations and guesses are used, and there are always risks of human error and differing concepts of risk. So, the financial managers should plan the capital budgets for ten years in advance.

Administrations generally consider the questions of the urgency or otherwise of proposals. This urgency refers to the degree of necessity, and indicates that certain projects are essential to the survival of a firm and that, therefore, they should be exempted from the rigours of objective evaluation.

Accounting Criterion:

With the help of accounting criterion, project profitability is measured in the annual percentage of capital employed. This is often referred to as the accounting rate of return.

Engineering Methods:

There are two engineering methods. The first one, known as the Hoskold method, requires that uniform deposits be made in a sinking fund, which may earn a specified rate of return so that, at the end of the assets’ useful life, its value is equal to the amount required for replacing the asset.

The other one is known as undiscounted benefit-cost ratio (BCR). It is a ratio of the total benefits and costs involved in a particular investment project. No discount for futurity, business and financing risks is considered.

It is desirable that business managers should be able to appraise, from a critical viewpoint, the various techniques which may be applied to capital projects. The complexities of the methods can be left to experts. Basically, all the techniques are related to a return on the original investment.

The major difference of approach is that some businesses relate expected profit to the investment and others relate the cash flow to the original investment. Although cost is an important factor in deciding the method of financing, equally important is the consideration of retaining control or of avoiding risks.

Fallacies in Analysing Capital Budgeting Proposals

Fallacies in analysing capital budgeting proposals are given below:

1. No Alternatives

Perhaps the most common mistake in analysing a capital proposal is the failure to consider alternatives.

2. ‘Must’ Investment

Closely related to this is the ‘must’ investment fallacy. The common conviction that certain equipment replacements are indispensable for continuing operations implies that the top management has no alternative.

3. High Strategy

Another fallacy is the notion that some projects are so pivotal for the long-run welfare of an enterprise and that they possess a high strategic value which overrides mere economic considerations and lifts their evaluation into a mystic realm beyond the ken of economic and financial analysis.

4. Routine Replacement

This fallacy maintains that scheduled periodic replacements of capital facilities are practical and inexpensive substitutes for an investment analysis of the economic desirability of individual replacement.

5. Prediction is Impossible

Scoffers maintains that since the future cannot be predicted with accuracy, it is futile to try to guess the utility of a proposal or to project its earnings beyond the first year.

6. Fair share of Overheads

A common error in project analysis is to use allocations of current overheads instead of estimating the added costs that would be caused by the project.

7. Free Ride

This ‘free ride’ fallacy leads to the conclusion that earnings from expansion investments are almost equivalent to their revenue.

8. Carrying Charge

The practice of charging the earnings of all projects with an interest cost might be called the ‘carrying charge’ fallacy. Usually this charge is computed by applying the company’s short-term borrowings rate to the capitalised portion of the original investment.

9. Book Value

The book value concept excludes outlays that are expanded (rather than capitalised) from the amount of investment serving as the base for the rate-of-return estimate.

10. Taxes Don’t Matter

There is a surprisingly widespread conviction that adjustments for corporate income taxes are an academic matter.

Capital Budgeting – Fundamentals of Evaluating Foreign Projects

Once a firm has compiled a list of prospective investments, it uses capital budgeting techniques to select from among them that combination of projects which maximizes the firm’s value to shareholders.

The theoretical framework involved in evaluation of domestic projects is the same as for foreign projects and various considerations influencing choice of a project within the country are the same as those for projects overseas. However, there are a host of factors that are unique to foreign investment that render cross-border investment decisions complicated.

Precisely speaking, the basic steps involved in evaluation of a project are:

1. Determine net investment outlay;

2. Estimate net cash flows to be derived from the project over time, including an estimate of salvage value.

3. Identify the appropriate discount rate for determining the present value of the expected cash flows.

4. Apply NPV or IRR to determine the acceptability or priority ranking of potential projects.

The evaluation process becomes complicated because of the factors peculiar to international operations.

Tax Implications on Capital Budgeting

There are two stages for taxation in a capital project. First, is the initial project cost and the other one is in its operation after the project has started functioning.

Various taxes involved in the project in its initial stages are:

i. Excise duty

ii. Sales tax

iii. Works contract tax

iv. Entry tax

v. Customs duty

vi. Service tax

vii. Income tax

viii. R&D cess.

During the operation cycle too, the same taxes are involved. These taxes are added to the operating cost.

The tax aspects, which need a managerial examination and review are:

i. Location of projects

ii. Mode of financing

iii. Mode of execution

iv. Type of project to be executed

v. Mode of procurement

vi. A project in a running organisation

vii. A new project as a new company

viii. Procurements from small-scale units

ix. Free issue of materials to the construction contractors, etc.

These aspects in projects are to be examined for availing the tax benefit to the extent possible.

Capital Budgeting in Practice

Capital budgeting differs quite widely between companies and countries.

However, some common tendencies have been identified in different studies and they have been briefly explained in the following lines:

First, let us take the question of generation of investment ideas. It has been generally found that small proposals of cost reduction or replacement or rejuvenation of plant and equipment do generally originate at the plant level and they go upwards for their approval. The proposals need to be supported by justification for the expenditure in terms of likely benefits from this expenditure.

On the basis of these proposals, the top management takes its decision after proper review/ vetting at several levels. The proposals for diversification and expansion originate at the top level and are finally accepted or rejected after a due process of appraisal and consultations at various levels in an organisation.

The executives often do not have clarity about the concept of cash flows and the principles of estimating cash flows such as taking incremental, after tax cash flows, taking the opportunity cost and ignoring the sunk cost etc. The need for additional working capital is often ignored.

Another problem with estimating cash flows is that it is not easy to give a forecast of the next 10 years because the future is uncertain and nobody wishes to make estimates for such a long period, lest they go wrong. Although cash outflows on plant machinery, installation etc. appear to be relatively certain but in actual practice, big projects often take 2-3 years of time in their completion and time and cost overruns are not uncommon.

This makes the job of cash flow forecasting still more difficult. The evaluation of cash flows and their adjustment for time value is again a formidable task, because the rate of discount or weighted average cost of capital cannot be easily calculated at the proposal stage itself. In the absence of a given rate of discount the evaluation of cash flows cannot be done easily.

Now, let us take the method of evaluation. It has been repeatedly pointed out that payback, and ARR are not scientific and NPV, IRR and PI are the best. However, in reality payback and ARR are very commonly used in practice. This is true both in India and abroad.

Payback is used in practice very commonly for several reasons. Firstly, it is simple to understand and easy to calculate. Secondly, it involves estimation of cash flows in the first few years only rather than over the entire life of an asset (which it may not be possible to do because the working life of a machine may be 10-15 years).

Thirdly, since the payback is insisting on early recovery of capital, it is automatically taking care of risk factors. It has been found that in small value investments, the decision is invariably on a payback basis, while in large investments other more elaborate and scientific methods are used.

ARR is also sometimes used because of several factors. Firstly, people are more accustomed to Income Statement, P&L a/c etc. rather than cash flow statements. Secondly, it may be projected for the future on the basis of the first few years, whereas NPV calculation needs data for the entire life of an asset including its scrap value at the end.

Thus, calculating ARR seems relatively easy. Thirdly, it is more appealing to the executives, because the objective of a firm is to increase profit and ARR is a measure of profitability.

Moreover, the practice of many financial institutions, requiring the prospective borrowers to give a projected P&L a/c and Balance Sheet for the next few years, has strengthened the need for projected accounting data. Many financial institutions also want a projected ‘Return on Capital Employed’ (ROCE) for the next few years, as a measure of future profitability.

The scene is however, changing and due importance is being given to the modern techniques, often as supplement to the traditional methods. The financial institutions also now ask for the IRR of the proposed project proposal, before accepting it for further examination.

NPV may, then, be calculated on the basis of cost of capital. In fact, instead of relying upon any one method, the practice is to test a proposal from several techniques and then decide accordingly.

Risk consideration in practice is very difficult. One simplest method, as described above is to insist on shorter payback. Other methods are conservative estimates and sensitivity analysis.

While the objective of shorter payback and conservative estimates is to create a safety margin or a cushion, in sensitivity analysis, the objective is to see the impact of change of key variables, like the discount rate, output level, price, cost etc. and then take decision accordingly.

Risk adjusted discount rate is also used for capital budgeting of risky projects. We must understand that no one method can be taken as perfect in all the situations and adjustment in methodology and key variables may be required to be done in some cases.

Thus, capital budgeting in practice is sometimes different from the theoretically best methods. This is probably because the real world is much more difficult than we assume it to be while developing a model. The ideal course is to know all the theoretically best methods and then try to apply them as far as possible, and practicable. Use of multiple methods is also a safeguard against excessive reliance on any one method. This is the golden rule.

Capital Budgeting Problems

Problems in Capital Budgeting:

The analytical techniques (investment return and time) are, to some extent, estimates. Even with all the ‘knowledgeable factors’ collected and duly analysed, there are many unknown factors which cannot be foreseen, controlled or avoided.

Financial planning for liquidity and profitability is fraught with many of the same risks that apply to other phases of business activity. Preparation is essential for the same types of adjustments. The risks of faulty projection of financial requirements are particularly great in the planning of capital expenditures for long-term fixed asset expansion.

It is necessary to look for some non-figure aspects of the projects under consideration. Managers should not fail to consider that one project may fit in better with a company’s goals or that the effect on employee morale would be profound if a new piece of equipment is introduced or a new technique is used.

Often enough, it is dangerous to assume that mathematically exact techniques always produce highly accurate results. Caution must be exercised in the application of methods to problems of capital expenditure.

Capital investment can be determined in some cases with a high degree of accuracy; but in the development of a new product, or in the opening of a new sales territory, the amount can only be approximated.

Returns, such as savings, earnings etc. depend upon estimates which may be inaccurate.

To estimate the useful or economic life of an investment is perhaps the most tenuous thing.

Contrasting capital budgeting practices with theory reveals a number of differences. This is most apparent in selection, which has been a primary focus of financial theory and the most closely examined aspect of business practice.

Differences exist but are less closely examined at the other stages as well. Thus, in contrast to theoretical assumptions, many projects are rejected during the pre-selection stages apparently for non-economic considerations (for example, personalities and inter departmental politics).

Also, since the role of finance at this stage is minor, it is possible, considering the problems companies have with incremental costing, that some projects are mistakenly rejected (accepted) because of mis-allocated costs. Companies may not always use cash flows and when they do, they overlook some components in developing those flows.

In the selection of proposals, contradictions are most evident.

These include the following:

(a) The use of discounted cash of low techniques is now a rule rather than an exception, but it is the internal rate of return (not the net present value technique) that has gained acceptance in business.

(b) Despite many years of disagreement, payback period has still been widely used,

(c) Capital rationing is common place. Such a condition is at odds with the financial market equilibrium theories. In theoretical prescription for optimization under capital constraints, linear programming is infrequently used.

(d) Companies use cost of capital but not in a manner suggested by theory,

(e) Risk analysis models are yet to be accepted universally. Many companies simply change the required payback period to adjust for risks.

The majority of companies appear to conduct post-audits. However, ROI-type measures are the most frequently reported basis of performance measurement. Such procedures are inconsistent with the use of DCF techniques for selection. They may encourage managers to concentrate on short-run profitability at the expense of the long-term goals of the companies and are likely to be dysfunctional.

Tarun Mukherjee and Glenn V. Henderson observe that the management’s primary goal is to maximise the wealth of the firm’s shareholders. Capital budgeting theory prescribes decision rules in keeping with this objective.

According to the theory, the firm’s goal should be to maximise the wealth of its shareholders. The theory has formulated selection rules consistent with this goal. Wealth maximization has implications in different stages.

In the identification stage, the theory implicitly assumes that all projects are evaluated on the basis of economic merit. In the development stage, an implication is that all feasible ideas are developed into full-blown proposals and none is accepted (or rejected) for. The theory considers incremental after-tax cash flow as the correct definition of benefits for capital budgeting analysis.

Proper estimation of cash flow requires quantification of project ramifications including impact on sales of other company products, working capital requirements and reactions from competitors. In selection, the theory suggests the use of discounted cash flow (DCF) techniques and more specially, use of net present value (NPV) analysis.

Theoretically, capital rationing (rejection of positive NPV projects that are not displaced by directly competing, mutually exclusive alternatives) should not exist in efficient capital markets. In such a market, funds should be available for any project that promises returns in excess of an appropriate risk-returns rate.

It is presumed that a publicly held company continues investing as long as the expected rate of return from a project is higher than its required rate. Holding back on otherwise positive NPV projects runs counter to the wealth-maximising objective. Methods used to review investment decisions (in the control phase) should be consistent with those used for selection.

If DCF methods are theoretically correct for selection, methods which consider the time value of money should be used to monitor implemented projects and to evaluate managerial performance.

Capital Budgeting Limitations

The capital budgeting process suffers from the following inherent limitations:

Limitation # (a) Difference in Actual and Estimation:

The evaluation of an investment proposal by the capital budgeting process is based on the estimated economic life of the project. The annual cash inflows, which are crucial to the acceptance decision, are only estimation. The actual economic life of the project may either exceed or fall short of the estimations.

Likewise, the actual annual cash inflows may be either more or less than their estimates. As a result, a good investment may be rejected while a bad proposal may be accepted, besides losing control over an accepted project.

Limitation # (b) Ignores Qualitative Aspects:

There are certain factors like morale of the employees, goodwill of the firm, etc., which cannot be correctly quantified but influence the capital budgeting decision. The capital budgeting process fails to take into consideration such qualitative aspects of an investment project, in spite of their crucial role in successful and profitable implementation of such project. As a result, true worth and profitability of the project stands compromised.

Limitation # (c) Inappropriate Assumption:

It is assumed that various investment proposals under consideration are mutually exclusive. This may not be practically true in some circumstances under which there are dependent projects. It is also not appropriate to assume that mathematically exact techniques always produce highly accurate results.

Limitation # (d) Subjectivity:

Capital budgeting process in case of investment proposals requires the estimation of discount factor to compute the required rate of return. This discount factor remains highly subjective to the perception of the finance manager, thus, exposing the firm to adverse consequences of an erroneous estimation.

Cookie	Duration	Description
cookielawinfo-checkbox-analytics	11 months	This cookie is set by GDPR Cookie Consent plugin. The cookie is used to store the user consent for the cookies in the category "Analytics".
cookielawinfo-checkbox-functional	11 months	The cookie is set by GDPR cookie consent to record the user consent for the cookies in the category "Functional".
cookielawinfo-checkbox-necessary	11 months	This cookie is set by GDPR Cookie Consent plugin. The cookies is used to store the user consent for the cookies in the category "Necessary".
cookielawinfo-checkbox-others	11 months	This cookie is set by GDPR Cookie Consent plugin. The cookie is used to store the user consent for the cookies in the category "Other.
cookielawinfo-checkbox-performance	11 months	This cookie is set by GDPR Cookie Consent plugin. The cookie is used to store the user consent for the cookies in the category "Performance".
viewed_cookie_policy	11 months	The cookie is set by the GDPR Cookie Consent plugin and is used to store whether or not user has consented to the use of cookies. It does not store any personal data.