There are two broad evaluation methods for a capital budgeting proposal:
i. Non-Discounted Cash Flow Methods:
These are the traditional methods and include payback period and the accounting rate of return (ARR). Their biggest disadvantage is that they ignore the time value of money. The payback method is skewed towards selection of projects with the shortest payback period; it ignores the timing of profits as well as expected profits after the payback period.
The ARR is the average annual expected profits from the project divided by the project cost. It is superior to the payback method because it considers all future profits but its value is affected by computation—average pre-tax profits and average project cost will generate a higher ARR than post-tax profits and total project cost.
ADVERTISEMENTS:
ii. Discounted Cash Flow (DCF Methods):
They take into account time value of money. The methods include net present value, internal rate of return, and profitability index. All three methods consider the time value of money, use post-tax cash flows, and consider all cash flows over the project’s life. They are therefore superior to traditional evaluation methods.
Political Risk:
Overseas project proposals have to contend with changes in political risk in the host country. For a particular proposal, a company may consider multiple locations in several countries, each of which has different levels of political risk. Political risk is dynamic and can alter over the project’s life. This affects the usefulness of a country wise ex ante assessment. The company has to carefully deliberate on whether or not it should entertain a host country as a location, and the financial and strategic payoffs of doing so.
ADVERTISEMENTS:
The company has to spend resources in order to make estimates of cash flows and the riskiness of foreign direct investment in that country. Deliberation costs vary with the political risk of the host country. The higher the political risk, the higher are an MNC’s deliberation costs.
MNCs rely on quantitative and qualitative data from multiple sources of information to make political risk assessment:
i. Internal Information:
This is a combination of existing knowledge in the parent company, and streaming information by employees working in the host country or the region.
ADVERTISEMENTS:
ii. External Sources:
They include information collected from vendors, bankers, country rankings, and sovereign credit ratings by rating agencies such as Standard and Poor, Moody and Euromoney (which provides bi-annual rankings of countries). Euromoney assigns a 30% weight to political risk (a few the other factors for which weights are assigned, are economic performance, and access to capital markets and bank finance). The factors taken into consideration to assess the level of political risk include stability of the government and perception about corruption, the judicial system, and transparency.
Sovereign ratings are extremely important because they shape the perceptions of overseas investors about a country’s risk climate, and affect cost of capital. In 2009, S&P retained India’s long-term rating of’ BBB-‘ (and short-term rating of ‘A-3’). In March 2010, it raised its rating outlook for India from ‘negative’ to ‘stable’, while Moodys upgraded India’s rating in July 2010 to ‘Bal’. When a country’s sovereign rating rises, its companies can raise funds overseas at lower rates.
When DCF methods are used to evaluate an overseas investment proposal, political risk is incorporated into the evaluation process either by increasing the discount rate or decreasing forecasted cash flows. When deliberation costs are high, firms prefer non-DCF methods. Even when the payback method is used, political risk is accommodated by shortening the payback period, and when ARR is used, it is accommodated by increasing the cut-off rate.
ADVERTISEMENTS:
Traditional methods and DCF methods are complements rather than substitutes, and there are regional variations with respect to manager preferences. Managers in North America and Latin America prefer ‘sophisticated’ capital budgeting techniques (NPV and IRR), and IRR is more popular than NPV. Fortune 1000 companies prefer to use the NPV. There is mixed evidence when it comes to Asia—managers in a few countries prefer DCF methods, .while managers in others prefer traditional methods, or give equal importance to both.
Computation of Cash Flows:
A capital budgeting proposal requires an outflow of cash, either at the beginning of the project itself (initial outlay) or over the first few years. Depreciation (D) is a non-cash expense. The amount of depreciation per annum is known at the outset, based upon the depreciation method the company follows (such as the straight line method, or the written down value method).
Earnings before Depreciation and Taxes (EBDT) are revenues minus costs before deducting depreciation and corporate income tax payable. Earnings Before Tax (EBT) is the EBDT minus depreciation. Earnings after Tax (EAT) is EBT minus the tax payable. Cash Flows After Tax (CFAT) is earnings after tax (EAT) plus depreciation.
ADVERTISEMENTS:
EAT = (EBDT – D) (1 – T) where ‘T’ is the tax rate
CFAT = EAT + D
or CFAT = (EBDT – D) (1 – T) + D
Cost of Capital:
ADVERTISEMENTS:
It is the weighted average cost of capital (WACC).
Given cost of equity (ke), the after-tax cost of debt (kd), and weights of equity and debt (we and wd respectively), the WACC is:
WACC = (ke) (we) + (kd) (wd)
Under the NPV method, the cost of capital is the discount rate used to compute the present value of after-tax cash flows. Under IRR, the cost of capital is the hurdle rate against which the project’s IRR is compared.
ADVERTISEMENTS:
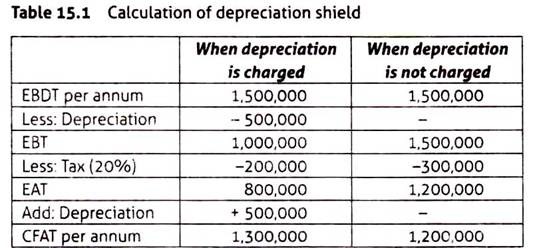
Depreciation Shield and Interest Shield:
Depreciation decreases corporate tax payable (Table 15.1). The depreciation shield is the product of annual depreciation and the corporate tax rate. Assume that the expected annual earnings before depreciation and taxes (EBDT) over a project’s five-year life are Rs. 1.5 million, the corporate tax rate (Tr) is 20 %, and the annual depreciation (D) is Rs. 500,000. The depreciation shield is calculated as (D) (Tr) is Rs. 100,000.
It is the difference between tax payable when there is no depreciation and the tax payable when there is depreciation (300,000 – 200,000 = 100,000). The annual depreciation shield over the proposed project’s life is affected by the depreciation method (straight line method, or written down value method) and the corporate tax rate expected to be in force over the project’s life.
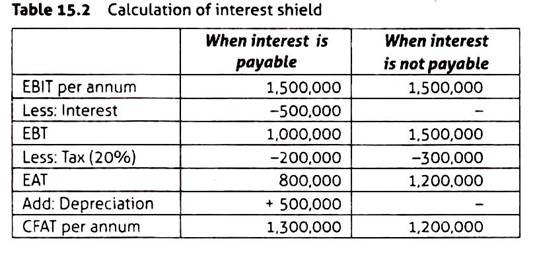
Interest shield, computed as (I)(Tr) is shown in Table 15.2. The use of debt (and therefore payment of interest) is a financing decision which reduces the tax payable.
Adjusted Present Value:
ADVERTISEMENTS:
The NPV is not equipped to deal with the issues described above. A technique that incorporates all these aspects into the evaluation process was proposed by Lessard (1979), and it is called the adjusted present value (APV). The APV adopts a ‘divide and conquer’ approach and recognizes the financial contributions to a project’s value ‘separately and explicitly’.
The total present value is the sum of the remittable project cash flows, the interest shield, the value of the subsidized loan, and other special situations encountered only in foreign projects. The accept/reject decision in APV is identical to that under NPV- accept the project if the APV is positive and reject it when the APV is negative.
For each of the issues discussed in the previous section, APV adopts the following rules:
1. Divide cash flows and tax savings into risky and less risky groups.
2. Consider the cash flows after deducting the reduction in sales revenues due to the commissioning of the project
ADVERTISEMENTS:
3. Consider remittable cash flows.
4. Estimate future exchange rates.
If the purchasing power parity theory is being used to determine the exchange rates, the exchange rate at the end of each year ‘t’ is:
E(SH/F)t = SH/F (1 + IH] ÷ [1 + IF])t
where E(S H/F)t is the expected spot rate at the end of year ‘t’
SH/F is the current spot rate
ADVERTISEMENTS:
IH is the expected inflation rate in the home country
IF is the expected inflation rate in the foreign (host) country
5. Use the higher of the two corporate tax rates to determine after tax cash flows.
6. Calculate the value of subsidies offered by the host country.
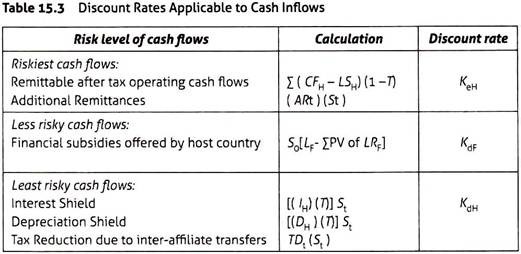
7. Use different discount rates for different components of cash flows to take into account their level of riskiness. – use cost of equity in the home country as the discount rate for riskiest cash flows, use the market rate of borrowing in the foreign country as the discount rate for less risky cash inflows, and use cost of debt in the home country as the discount rate for least risky cash flows (Table 15.3). Compute cost of equity using the Capital Asset Pricing Model (CAPM) Ke = rf + B (rm + rf), using the market rate of return and the risk-free rate in the home country.
8. Treat funds moved through transfer pricing as a separate stream of cash flows.
ADVERTISEMENTS:
9. Treat funds moved through additional remittances as a separate stream of cash flows.
10. Reduce activated funds from the initial outlay.
APV is calculated as:
APV = {[∑PV( CFH – LSH) (1 – T)] + [∑PV (St) [(Dt) (T)] + [∑PV (IH) (T) + S0 [LF – ∑PVLRF] + [∑PV (TDt) (St)] + [∑PV (ARt) (St)] – [S0 (C – AF0)]}
S0 is SH/F (the exchange rate) at beginning of the initial year
St is SH/F (the exchange rate) at the end of year t.
ADVERTISEMENTS:
H is-home currency of the parent company
F is foreign currency of the host country
CFH are cash inflows converted into home currency
LSH is the profit from sales lost in the host country (when the project begins commercial production and sales) converted into home currency
C is initial outlay
AF0 is activated funds at the beginning of the project
Dt is depreciation per annum in year t
It is interest per annum in year t
T is the higher of home country tax rate and host country tax rate
TDt is tax savings from movement of funds in year ‘t’, through transfer pricing, by an affiliate in a higher tax environment to an affiliate in a lower tax environment.
ARt is additional remittances at time ‘t’. It is the repatriation of income in year ‘t’ by the affiliate to the parent company by evading repatriation regulations in the foreign country.
LF is the face value of the subsidized loan expressed in foreign currency.
LRF is the loan repayment expressed in foreign currency.
∑PV(CFH – LSH)( 1 – T) is the sum of the present value of net after-tax remittable cash flows expressed in the home currency.
∑PV(St) [(Dt)(T)] is the sum of the present value of the depreciation tax shield.
∑PV (IH) (T) is the sum of the present value of the interest tax shield.
S0[LF – ∑PVLRF ] is the value of a financial subsidy. The market cost of borrowing in the foreign country is the discount rate used to determine the present value of the loan repayment (LRF).
∑PV(TDt) (St) is the sum of the present value of tax reduction due to inter-subsidiary transfers
∑PV(ARt) (St)] is the sum of the present value of additional remittances.
[S0 (C – AF0 )] is the net initial outflow.
KeH is the home country cost of equity; KdF is the host country cost of debt; KdH is the risk-free rate in home country
How is APV Calculated?
1. Determine the net initial cash outflow (C – AF0)
2. Choose the relevant tax rate.
3. Determine remittable cash flows (CFH – LSH)t (1 – T), depreciation shield (Dt)(T), interest shield (IH ) (T), financial subsidy [LF – ∑PV of LRF], tax reduction due to inter- subsidiary transfers (TDt)(St)and additional remittances (ARt).
4. Estimate the exchange rate at the end of each year of the life of the proposal. Express the net initial cash outflow and all the values in the previous step in the parent company’s home currency.
5. Choose discount rates appropriate to the risk level of each cash inflow, in order to determine the present value of the cash inflows.
6. Find the APV. Accept the project if APV is positive, reject it if APV is negative.
Illustration:
An Indian MNC is considering a project proposal for setting up a manufacturing facility in Mexico. It has accumulated 77,226 pesos over the years, which can be used to finance this project. The project has a life of 10 years and an estimated initial cost of the project is 1 million pesos. The current exchange rate is INR 12/MXN. Calculate the net initial outflow for the project.
Solution:
Given the estimated initial cost = 1 million pesos, activated funds 77,226 pesos
Net initial outflow = total project cost – value of activated funds = 1,000,000 – 77,226 = 922,774 Pesos
Net initial outflow in rupees = (Rs. 12) (922,774 pesos) = Rs. 11,073,288
Comparison of NPV and APV:
Both NPV and APV are discounted cash flow techniques used to evaluate capital budgeting proposals.
But they have some fundamental differences:
i. The NPV method treats all cash inflows as identical in terms of their risk profile. The APV categorizes cash inflows so as to accommodate the unique issues confronted by evaluators in an overseas capital budgeting proposal.
ii. The NPV uses a single discount rate, namely the weighted average cost of capital (WACC) for finding the present value of cash inflows. But the APV differentiates between the risk levels of cash inflows. The riskiest inflows are discounted at a higher rate (the cost of equity), and the less risky ones at the cost of debt or the risk-free rate.
The value of a financial subsidy is discounted at the market rate of borrowing in the foreign country (that is, the host country). The APV uses a cost of equity based on the value of beta (systematic risk) derived from the MNC’s stock price in the home country. But this may not adequately reflect the risk level in the foreign country.