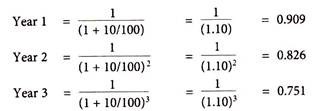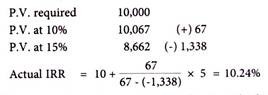The following points highlight the top seven methods used for evaluating the investment proposals by a company. The methods are: 1. Payback Period Method 2. Accounting Rate of Return Method 3. Net Present Value Method 4. Internal Rate of Return Method 5. Profitability Index Method 6. Discounted Payback Period Method 7. Adjusted Present Value Method.
1. Payback Period Method:
The payback period is usually expressed in years, which it takes the cash inflows from a capital investment project to equal the cash outflows. The method recognizes the recovery of original capital invested in a project. At payback period the cash inflows from a project will be equal to the project’s cash outflows.
This method specifies the recovery time, by accumulation of the cash inflows (inclusive of depreciation) year by year until the cash inflows equal to the amount of the original investment. The length of time this process takes gives the ‘payback period’ for the project. In simple terms it can be defined as the number of years required to recover the cost of the investment.
In case of capital rationing situations, a company is compelled to invest in projects having shortest payback period. When deciding between two or more competing projects the usual decision is to accept the one with the shortest payback. Payback is commonly used as a first screening method. This method recognizes the recovery of the original capital invested in a project.
ADVERTISEMENTS:
Merits:
The merits of payback period method are as follows:
1. It is simple to apply, easy to understand and of particular importance to business which lack the appropriate skills necessary for more sophisticated techniques.
2. In case of capital rationing, a company is compelled to invest in projects having shortest payback period.
ADVERTISEMENTS:
3. This method is most suitable when the future is very uncertain. The shorter the payback period, the less risky is the project. Therefore, it can be considered as an indicator of risk.
4. This method gives an indication to the prospective investors specifying when their funds are likely to be repaid.
5. Ranking projects according to their ability to repay quickly may be useful to firms when experiencing liquidity constraints. They will need to exercise careful control over cash requirements.
6. It does not involve assumptions about future interest rates.
ADVERTISEMENTS:
Demerits:
The payback period method suffers from the following drawbacks:
1. It does not indicate whether an investment should be accepted or rejected, unless the payback period is compared with an arbitrary managerial target.
2. The method ignores cash generation beyond the payback period and this can be seen more a measure of liquidity than of profitability.
ADVERTISEMENTS:
3. It fails to take into account the timing of returns and the cost of capital. It fails to consider the whole life time of a project. It is based on a negative approach and gives reduced importance to the going concern concept and stresses on the return of capital invested rather than on the profits occurring from the venture.
4. The traditional payback approach does not consider the salvage value of an investment. It fails to determine the payback period required in order to recover the initial outlay if things go wrong. The bailout payback method concentrates on this abandonment alternative.
5. This method makes no attempt to measure a percentage return on the capital invested and is often used in conjunction with other methods.
6. The projects with long payback periods are characteristically those involved in long-term planning, and which determine an enterprise’s future. However, they may not yield their highest returns for a number of years and the result is payback method biased against the very investments that are most important to long-term.
ADVERTISEMENTS:
Problem 1:
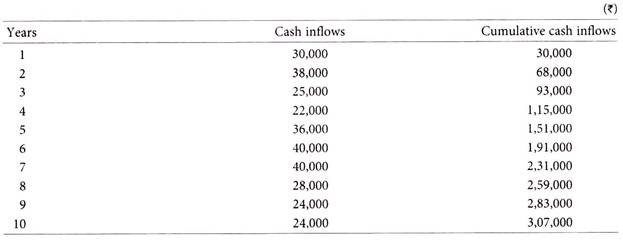
The project involves a total initial expenditure of Rs.2,00,000 and it is estimated to generate future cash inflow of Rs.30,000, Rs.38,000, Rs.25,000, Rs.22,000, Rs.36,000, Rs.40,000, Rs.40,000, Rs.28,000, Rs.24,000 and Rs.24,000 in its last year.
Solution:
Calculation of Payback Period:
In six years, Rs. 1,91,000 are recovered.
... Payback period = 6 years + Rs. 9,000/Rs. 40,000 x 12 months = 6 years 3 months
2. Accounting Rate of Return Method:
The accounting rate of return is also known as ‘return on investment’ or ‘return on capital employed’ method employing the normal accounting technique to measure the increase in profit expected to result from an investment by expressing the net accounting profit arising from the investment as a percentage of that capital investment. The method does not take into consideration all the years involved in the life of the project.
In this method, most often the following formula is applied to arrive at the accounting rate of return:
Sometimes, initial investment is used in place of average investment. Of the various accounting rates of return on different alternative proposals, the one having highest rate of return is taken to be the best investment proposal.
Merits:
The merits of accounting rate of return method are as follows:
1. It is easy to calculate because it makes use of readily available accounting information.
2. It is not concerned with cash flows but rather based upon profits which are reported in annual accounts and sent to shareholders.
ADVERTISEMENTS:
3. Unlike payback period method, this method does take into consideration all the years involved in the life of a project.
4. Where a number of capital investment proposals are being considered, a quick decision can be taken by use of ranking the investment proposals.
5. If high profits are required, this is certainly a way of achieving them.
Demerits:
The demerits of accounting rate of return method are summarized as follows:
1. It does not take into accounting time value of money.
ADVERTISEMENTS:
2. It fails to measure properly the rates of return on a project even if the cash flows are even over the project life.
3. It uses the straight line method of depreciation. Once a change in method of depreciation takes place, the method will not be easy to use and will not work practically.
4. This method fails to distinguish the size of investment required for individual projects. Competing investment proposals with the same accounting rate of return may require different amounts of investment.
5. It is biased against short-term projects in the same way that payback is biased against longer-term ones.
6. Several concepts of investment are used for working out accounting rates of return.
7. The accounting rates of return does not indicate whether an investment should be accepted or rejected, unless the rates of return is compared with the arbitrary management target.
ADVERTISEMENTS:
Problem 2:
A machine is available for purchase at a cost of Rs.80,000. We expect it to have a life of five years and to have a scrap value of Rs.10,000 at the end of the five year period.
We have estimated that it will generate additional profits over its life as follows:
These estimates are of profits before depreciation. You are required to calculate the return on capital employed.
Solution:
ADVERTISEMENTS:
Total profit before depreciation over the life of the machine = Rs.1,10,000
... Average profit p.a. = Rs.1,10,000/5 years = Rs.22,000
Total depreciation over the life of the machine = Rs.80,000 – Rs.10,000 = Rs70,000
... Average depreciation p.a. = Rs.70,000/5 years = RS.14,000
... Average annual profit after depreciation = Rs.22,00 – Rs.14,000 = Rs.8,000
Original investment required
ADVERTISEMENTS:
... Accounting rate of return = (Rs8,000/Rs.80,000) × 100 = 10%
Average investment = (Rs.80,000 + Rs.10,000)/2 = Rs.45,000
Accounting rate of return = (Rs.8,000/Rs.45,000) × 100 = 17.78%
3. Net Present Value Method:
The objective of the firm is to create wealth by using existing and future resources to produce goods and services. To create wealth, inflows must exceed the present value of all anticipated cash outflows. Net present value (NPV) is obtained by discounting all cash outflows and inflows attributable to a capital investment project by a chosen percentage e.g., the entity’s weighted average cost of capital.
The method discounts the net cash flows from the investment by the minimum required rate of return, and deducts the initial investment to give the yield from the funds invested. If yield is positive the project is acceptable. If it is negative the project in unable to pay for itself and is thus unacceptable. The exercise involved in calculating the present value is known as ‘discounting and the factors by which we have multiplied the cash flows are known as the ‘discount factors’.
Discount factor = 1/(1+r)n
Where, r = Rate of interest p.a.
n = number of years over which we are discounting.
Discounted cash flow is an evaluation of the future net cash flows generated by a capital project, by discounting them to their present day value. The method is considered better for evaluation of investment proposal as this method takes into account the time value of money as well as, the stream of cash flows over the whole life of the project. The discounting technique converts cash inflows and outflows for different years into their respective values at the same point of time, allows for the time value of money.
Merits:
Conceptually sound, the net present value criterion has considerable merits:
1. It explicitly recognises the time value of money.
2. It considers the cash flow stream in its entirety.
3. It squares neatly with the financial objective of maximization of the wealth of stockholders. The net present value represents the contribution to the wealth of stockholders.
4. The net present value (NPV) of various projects, measured as they are in today’s rupees, can be added.
For example, the NPV of a package consisting of two projects A and B, will simply be the sum of NPV of these projects individually:
NPV(A + B) = NPV(A) + NPV(B)
The additivity property of NPV ensures that a poor project (one which has a negative NPV) will not be accepted just because it is combined with a good project (which has a positive NPV).
5. A changing discount rate can be built into NPV calculations by altering the denominator. This feature becomes important as this rate normally changes because the longer the time span, the lower is the value of money and the higher is the discount rate.
6. This method is particularly useful for the selection of mutually exclusive projects.
Demerits:
The demerits of NPV method are as follows:
1. It is difficult to calculate as well as understand and use.
2. The ranking of projects on the NPV dimension is influenced by the discount rate – which is usually the firm’s cost of capital. But cost of capital is quite a difficult concept to understand and measure in practice.
3. It may not give satisfactory answer when the projects being compared involve different amounts of investment. The project with higher NPV may not be desirable if it also requires a large investment.
4. It may mislead when dealing with alternative projects of limited funds under the condition of unequal lives.
5. The NPV measures an absolute measure, does not appear very meaningful to businessmen who think in terms of rate of return measures.
Problem 3:
A firm can invest Rs. 10,000 in a project with a life of three years.
The projected cash inflows are:
Year 1 – Rs.4,000,
Year 2 – Rs.5,000 and
Year 3 – Rs.4,000.
The cost of capital is 10% p.a. should the investment be made?
Solution:
Discount factors can be calculated based on Rs.1 received in with ‘r’ rate of interest in 3 years using 1/(1+r)n
In this article, the tables given at the end of the book are used wherever possible. Where a particular year or rate of interest is not given in the tables, students are advised to use the basic discounting formula as given above.
Analysis:
Since the net present value is positive, investment in the project can be made.
4. Internal Rate of Return Method:
Internal rate of return (IRR) is a percentage discount rate used in capital investment appraisals which brings the cost of a project and its future cash inflows into equality. It is the rate of return which equates the present value of anticipated net cash inflows with the initial outlay. The IRR is also defined as the rate at which the net present value is zero.
The rate for computing IRR depends on bank lending rate or opportunity cost of funds to invest which is often called as ‘personal discounting rate’ or ‘accounting rate’. The test of profitability of a project is the relationship between the IRR (%) of the project and the minimum acceptable rate of return (%).
The IRR can be stated in the form of a ratio as shown below:
P.V. of Cash Inflows – P.V. of Cash Outflows = Zero
The IRR is to be obtained by trial and error method to ascertain the discount rate at which the present values of total cash inflows will be equal to the present values of total cash outflows.
If the cash inflow is not uniform, then IRR will have to be calculated by trial and error method. In order to have an approximate idea about such discounting rate, it would be better to find out the ‘factor’. The factor reflects the same relationship of investment and cash inflows as in case of payback calculations.
F = I/C
Where, F = Factor to be located
I = Original Investment
C = Average cash inflow per year
In appraising the investment proposals, IRR is compared with the desired rate of return or weighted average cost of capital, to ascertain whether the project can be accepted or not. IRR is also called as ‘cut off rate’ for accepting the investment proposals.
Merits:
The merits of IRR method are as follows:
1. It considers the time value of money.
2. It takes into account the total cash inflows and cash outflows.
3. It is easier to understand. For example, if told that IRR of an investment is 20% as against the desired return on an investment is Rs.15,396.
Demerits:
The demerits of IRR method are given below:
1. It does not use the concept of desired rate of return, whereas it provides the rate of return which is indicative of the profitability of investment proposal.
2. It involves tedious calculations, based on trial and error method.
3. It produces multiple rates which can be confusing.
4. Projects selected based on higher IRR may not be profitable.
5. Unless the life of the project can be accurately estimated, assessment of cash flows cannot be correctly made.
6. Single discount rate ignores the varying future interest rates.
Problem 4:
A company has to select one of the following two projects:
Using the internal rate of return method, suggest which project is preferable.
Solution:
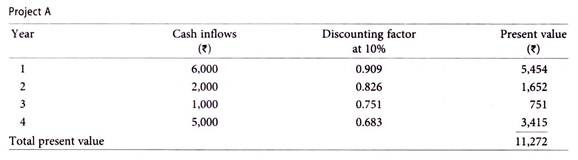
Average cash inflows of Project A = Rs.14, 000/4years = Rs.3, 500
Factor in case of Project A = 11,000/3,500 = 3.14
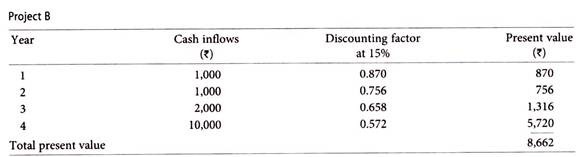
Average cash inflows of Project B = Rs.14, 000/4 years = Rs.3, 500
Factor in case of Project B = 10,000/3,500 = 2.86
The factor thus calculated will be located in table given at the end of the book on the line representing number of years corresponding to estimated useful life of the asset. This would give the expected rate of return to be applied for discounting the cash inflows in finding the internal rate of return.
In case of Project A, the rate comes to 10% while in case of Project B it comes to 15%.
The present value at 10% comes to Rs.11,272. The initial investment is Rs.11,000. Internal rate of return may be taken approximately at 10%. In case more exactness is required another trial rate which is slightly higher than 10% (since at this rate the present value is more than initial investment) may be taken.
Taking a rate of 12%, the following results would emerge
The internal rate of return is thus more than 10% but less than 12%.
The exact rate may be calculated as follows:
Since present value at 15% comes only to Rs.8,662. The initial investment is Rs.10,000. Therefore, a lower rate of discount should be taken. Taking a rate of 10% the following will be the result.
The present value at 10% comes to Rs.10,067 which is more or less equal to the initial investment. Hence, the internal rate of return may be taken as 10%. In order to have more exactness to internal rate of return, can be interpolated as done in case of Project ‘A’.
Analysis:
Thus, internal rate of return in case of project A’ is higher as compared to Project B. Hence, Project A is preferable.
NPV and IRR: Reasons for Conflict:
Both the NPV and the IRR methods are widely used for evaluation of projects, specially when the assessment is done by large organizations and the projects are large-scale. Both methods seek to assist management in their capital budgeting decisions.
The two methods may differ in the discounting rates applied to cash flows and in some basic assumptions on reinvestment of generated funds. Besides these, there are other points which lie at the root of the conflict between the two methods of evaluation.
The reasons for conflict between the NPV and the IRR methods are mainly as under:
1. NPV ranking depends on the discount rate used. Assuming the IRR for a project is 12%, then for a rate of discount greater than 12% no contradiction arises. However, if the discount rate used is less than 12%, the two methods of evaluation will give different rankings for the same project.
2. IRR expresses the result as a percentage rather than in money terms. Comparison of percentages may sometimes be misleading.
3. The implicit assumption of NPV is that cash flows from the project will be re-invested at the cost of capital.
4. Majority of the projects produce conventional cash flows, that is initial cash outflows followed by inflows in the subsequent years. If in the later years there are more number of net outflows, multiple IRRs will be produced.
Problem 5:
The NPV, IRR and other details of Project A and Project B are given below:
Which project do you suggest?
Solution:
If a choice has to be made between Project A and Project B because they are operationally mutually exclusive, the project chosen will depend upon the appraisal method used, because conflicting ranking will occur. Project B would be preferred based on NPV method, despite offering a lower percentage return on average, it involves investment of an extra Rs.11,000 – the return on which is sufficient to generate a further profit surplus (i.e., an increase in the NPV) when discounted at 10%.
Differential cash flows of Project A and Project B
Analysis:
Using IRR, Project A would be chosen because it provides a differential return in excess of the minimum required return. But with the simple observation of IRR between two projects. Project A will be selected because of its higher IRR of 23%.
5. Profitability Index Method:
It is a method of assessing capital expenditure opportunities in the profitability index. The profitability index (PI) is the present value of an anticipated future cash inflows divided by the initial outlay The only difference between the net present value method and profitability index method is that when using the NPV technique the initial outlay is deducted from the present value of anticipated cash inflows, whereas with the profitability index approach the initial outlay is used as a divisor.
In general terms, a project is acceptable if its profitability index value is greater than 1. Clearly, a project offering a profitability index greater than 1 must also offer a net present value which is positive. When more than one project proposals are evaluated, for selection of one among them, the project with higher profitability index will be selected.
Mathematically, PI (profitability index) can be expressed as follows:
This method is also called ‘benefit-cost ratio’ or ‘desirability ratio’ method.
Limitations:
The limitations of profitability index method are as follows:
1. Profitability index cannot be used in capital rationing problems where projects are indivisible. Once a single large project with high NPV is selected, the possibility of accepting several small projects which together may have higher NPV than the single project, is excluded.
2. Sometimes the project with lower profitability index may have to be selected if it generates cash flows in the earlier years, which can be used for setting up of another project to increase the overall NPV.
Problem 6:
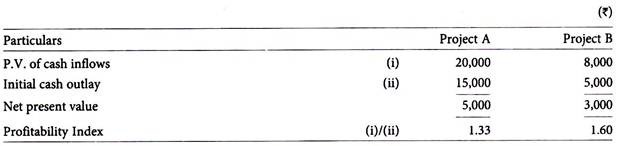
The NPV and profitability index of project A and project B are given below:
Which project can be selected based on the above data?
Solution:
According to the NPV method, Project A would be preferred, whereas according to profitability index Project B would be preferred. Although PI method is based on NPV, it is a better evaluation technique than NPV in a situation of capital rationing.
6. Discounted Payback Period Method:
In this method the cash flows involved in a project are discounted back to present value terms as discussed above. The cash inflows are then directly compared to the original investment in order to identify the period taken to payback the original investment in present values terms.
This method overcomes one of the main objections to the original payback method, in that it now fully allows for the timing of the cash flows, but it still does not take into account those cash flows which occur subsequent to the payback period and which may be substantial.
The method is a variation of payback period method, which can be used if DCF methods are employed. This is calculated in much the same way as the payback, except that the cash flows accumulated are the base year value cash flows which have been discounted at the discount rate used in the NPV method (i.e., the required return on investment).
Thus, in addition to the recovery of cash investment, the cost of financing the investment during the time that part of the investment remains unrecovered is also provided for. It thus, unlike the ordinary payback method, ensures the achievement of at least the minimum required return, as long as nothing untoward happens after the payback period.
Problem 7:
Geeta Ltd. is implementing a project with an initial capital outlay of Rs. 7,600.
Its cash inflows are as follows:
The expected rate of return on the capital invested is 12% p.a. Calculate the discounted payback period of the project.
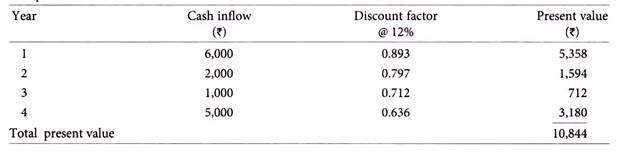
Computation of present value of cash flows:
Analysis:
The discounted payback period of the project is 3 years i.e., the discounted cash inflows for the first three years (i.e., Rs.5,358 + Rs.1,594 + Rs.712) is equivalent to the initial capital outlay of Rs.7,600.
7. Adjusted Present Value Method:
In the evaluation of capital budgeting proposals, the first step is to estimate the expected cash outflow and inflow of the project. Such estimates are made over economic life of the project and present values of future cash flows are reckoned. While calculation of present values of the future cash flows, otherwise called discounted cash flows, weighted average cost of capital (WACC) is considered as a rate for discounting the cash flows.
In NPV method, cash flows are discounted at WACC rate, and if the present value of cash inflow is higher than the present value of cash outflow, the project can be accepted. The rate of discounted return in the project with the initial outlay is calculated. Under IRR method this rate is the IRR of the project and it is then compared with WACC figure. If WACC of the project is lower than IRR, the project is accepted and vice versa.
Under adjusted present value (APV) approach, the project is splitted into various strategic components. The cash flow estimates of the project are first discounted at the cost of equity, and a base-case present value is arrived at as if the project is all-equity financed.
After that, the financial side effects are analyzed one by one and duly valued. For example, if the debt is proposed to be used as a component of capital, then positive impact of tax shield is added to the base-case present values. Likewise, different aspects in cost of financing like capital investment subsidy, flotation costs of public issue/rights issue, administrative cost of equity/debt funds are analyzed separately and a composite position arrived at.
The APV method is considered improvement over WACC method for the reason that by splitting the overall decision into logical pieces and attributing financial values to it, aid the management in correct valuation of the project’s viability. But this approach lays more emphasis on financial risk ignoring the business risk.
Under WACC approach, all flows are post-tax and the discount rate is also post-tax. Thus the benefit of tax shield will get discounted at the WACC. On the other hand, under APV approach, the tax shields are discounted back at the cost of debt.