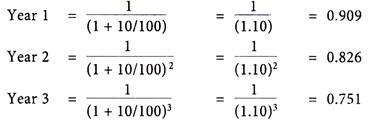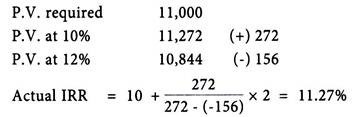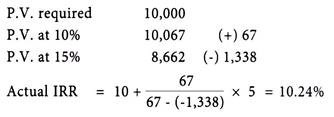The following points highlight the seven main methods used in determination of cash flow from business activities of a firm. The methods are: 1. Payback Period Method 2. Accounting Rate of Return Method 3. Net Present Value Method 4. Internal Rate of Return (IRR) Method 5. Profitability Index (PI) Method 6. Discounted Payback Period Method 7. Terminal Value Method.
1. Payback Period Method:
The payback period is usually expressed in years, which it takes the cash inflows from a capital investment project to equal the cash outflows.
The method recognizes the recovery of original capital invested in a project.
At payback period the cash inflows from a project will be equal to the project’s cash outflows.
ADVERTISEMENTS:
This method specifies the recovery time, by accumulation of the cash inflows (inclusive of depreciation) year by year until the cash inflows equal to the amount of the original investment.
The length of time this process takes gives the ‘payback period’ for the project.
In simple terms it can be defined as the number of years required to recover the cost of the investment.
In case of capital rationing situations, a company is compelled to invest in projects having shortest payback period.
ADVERTISEMENTS:
When deciding between two or more competing projects the usual decision is to accept the one with the shortest payback.
Payback is commonly used as a first screening method.
It is a rough measure of liquidity and rate of profitability.
This method is simple to understand and easy to apply and it is used as an initial screening technique.
ADVERTISEMENTS:
This method recognizes the recovery of the original capital invested in a project.
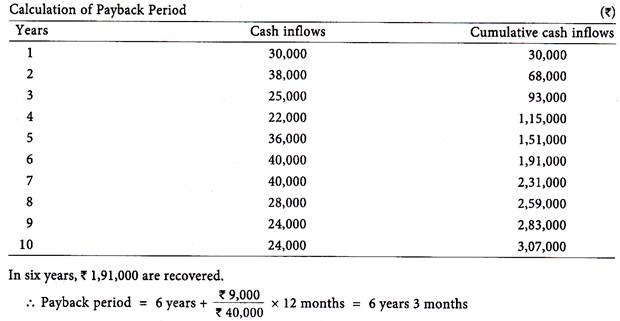
Illustration 1:
The project involves a total initial expenditure of Rs 2,00,000 and it is estimated to generate future cash inflow of Rs. 30,000, Rs. 38,000, Rs. 25,000, Rs. 22,000, Rs. 36,000, Rs. 40,000, Rs. 40,000, Rs. 28,000, Rs. 24,000 and Rs. 24,000 in its last year.
Solution:
2. Accounting Rate of Return Method:
The accounting rate of return is also known as ‘return on investment’ or ‘return on capital employed’ method.
It is a normal accounting technique to measure the increase in profit expected to result from an investment by expressing the net accounting profit arising from the investment as a percentage of that capital investment.
The method does not take into consideration all the years involved in the life of the project.
ADVERTISEMENTS:
In this method, most often the following formula is applied to arrive at the accounting rate of return.
Sometimes, initial investment is used in place of average investment.
Of the various accounting rates of return on different alternative proposals, the one having highest rate of return is taken to be the best investment proposal.
ADVERTISEMENTS:
For example, in three alternative proposals A, B and C with expected accounting rates of return of 10%, 20% and 18% respectively. Projects will be selected in order of B, C and A.
If the prevailing rates of interest is taken to be 15% p.a., only proposals B and C will qualify for consideration and in that order.
Illustration 2:
A machine is available for purchase at a cost of Rs 80,000. We expect it to have a life of five years and to have a scrap value of Rs. 10,000 at the end of the five year period.
ADVERTISEMENTS:
We have estimated that it will generate additional profits over its life as follows:
These estimates are of profits before depreciation. You are required to calculate the return on capital employed.
3. Net Present Value Method:
The objective of the firm is to create wealth by using existing and future resources to produce goods and services.
To create wealth, inflows must exceed the present value of all anticipated cash outflows.
ADVERTISEMENTS:
Net present value is obtained by discounting all cash outflows and inflows attributable to a capital investment project by a chosen percentage e.g., the entity’s weighted average cost of capital.
The method discounts the net cash flows from the investment by the minimum required rate of return, and deducts the initial investment to give the yield from the funds invested.
If yield is positive the project is acceptable.
If it is negative the project in unable to pay for itself and is thus unacceptable.
The exercise involved in calculating the present value is known as ‘discounting and the factors by which we have multiplied the cash flows are known as the ‘discount factors’.
The discount factor is given by the following expression:
ADVERTISEMENTS:
1/(1 + r)n
Where,
r = Rate of interest p.a.
n = number of years over which we are discounting.
Discounted cash flow is an evaluation of the future net cash flows generated by a capital project, by discounting them to their present day value.
The method is considered better for evaluation of investment proposal as this method takes into account the time value of money as well as, the stream of cash flows over the whole life of the project.
ADVERTISEMENTS:
One of the main disadvantages of both payback and accounting rates of return methods is that they ignore the fact that money has time value.
The discounting technique converts cash inflows and outflows for different years into their respective values at the same point of time, allows for the time value of money.
This method is particularly useful for the selection of mutually exclusive projects i.e. acceptance of one project amounts to rejection of the other project.
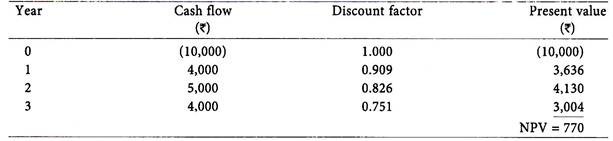
Illustration 3:
A firm can invest Rs. 10,000 in a project with a life of three years. The projected cash inflow are: Year 1 – Rs. 4,000, Year 2 – Rs. 5,000 and Year 3 – Rs. 4,000.
The cost of capital is 10% p.a. should the investment be made?
ADVERTISEMENTS:
Solution:
Firstly the discount factors can be calculated based on Rs. 1 received in with V rate of interest in 3 years.
The tables given at the end of the book are used wherever possible. Obviously where a particular year or rate of interest is not given in the tables, it will be necessary to resort to the basic discounting formula.
Analysis:
ADVERTISEMENTS:
Since the net present value is positive, investment in the project can be made.
4. Internal Rate of Return (IRR) Method:
IRR is a percentage discount rate used in capital investment appraisals which brings the cost of a project and its future cash inflows into equality.
It is the rate of return which equates the present value of anticipated net cash flows with the initial outlay.
The IRR is also defined as the rate at which the net present value is zero.
The rate for computing IRR depends on bank lending rate or opportunity cost of funds to invest which is often called as personal discounting rate or accounting rate.
The test of profitability of a project is the relationship between the IRR (%) of the project and the minimum acceptable rate of return (%).
The IRR can be stated in form of a ratio as shown below:
Cash Inflows/Cash Outflows = 1
P.V. of Cash Inflows − P.V. of Cash Outflows = Zero
The IRR is to be obtained by trial and error method to ascertain the discount rate at which the present values of total cash inflows will be equal to the present values of total cash outflows.
If the cash inflow is not uniform, then IRR will have to be calculated by trial and error method.
In order to have an approximate idea about such discounting rate, it will be better to find out the ‘factor’.
The factor reflects the same relationship of investment and cash inflows as in case of payback calculations.
F = I/C
Where, F = Factor to be located
I = Original Investment
C = Average cash inflow per year
In appraising the investment proposals, IRR is compared with the desired rate of return or weighted average cost of capital, to ascertain whether the project can be accepted or not.
IRR is also called as ‘cut off rate’ for accepting the investment proposals.
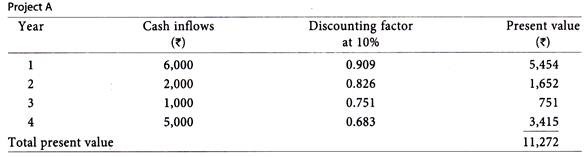
Illustration 4:
A company has to select one of the following two projects:
Using the internal rate of return method, suggest which project is preferable.
Solution:
Factor in case of Project A = 11,000/3,500 = 3.14
Factor in case of Project B = 10,000/3,500 = 2.86
The factor thus calculated will be located in table given at the end of the book on the line representing number of years corresponding to estimated useful life of the asset. This would give the expected rate of return to be applied for discounting the cash inflows in finding the internal rate of return.
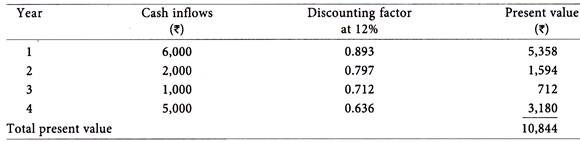
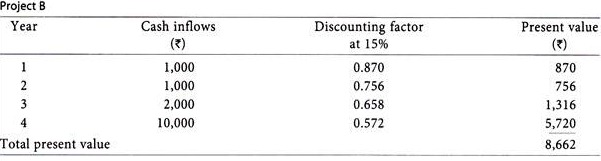
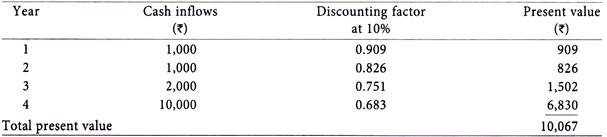
In case of Project A, the rate comes to 10% while in case of Project B it comes to 15%.
The present value at 10% comes to Rs. 11,272. The initial investment is Rs. 11,000. Internal rate of return may be taken approximately at 10%.
In case more exactness is required another trial rate which is slightly higher than 10% (since at this rate the present value is more than initial investment) may be taken.
Taking a rate of 12%, the following results would emerge:
The internal rate of return is thus more than 10% but less than 12%. The exact rate may be calculated as follows:
Since present vale at 15% comes only to Rs.8, 662, a lower rate of discount should be taken. Taking a rate of 10% the following will be the result:
The present value at 10% comes to Rs. 10,067 which is more or less equal to the initial investment. Hence, the internal rate of return may be taken as 10%.
In order to have more exactness to internal rate of return, can be interpolated as done in case of Project ‘A’.
Analysis – Thus, internal rate of return in case of Project ‘A’ is higher as compared to Project B. Hence, Project A is preferable.
5. Profitability Index (PI) Method:
It is a method of assessing capital expenditure opportunities in the profitability index.
The PI is the present value of an anticipated future cash inflows divided by the initial outlay.
The only difference between the net present value method and profitability index method is that when using the NPV technique the initial outlay is deducted from the present value of anticipated cash inflows, whereas with the profitability index approach the initial outlay is used as a divisor.
In general terms, a project is acceptable if its profitability index value is greater than 1.
A project offering a profitability index greater than 1 must also offer a net present value which is positive.
When more than one project proposals are evaluated, for selection of one among them, the project with higher profitability index will be selected.
Mathematically, PI can be expressed as follows:
PI = PV of Cash Inflows/PV of Cash Outlay
This method is also called ‘cost-benefit ratio’ or ‘desirability ratio’ method.
Illustration 5:
The following mutually exclusively can be considered:
Analysis – According to the NPV method, Project A would be preferred, whereas according to profitability index Project B would be preferred. Although PI method is based on NPV, it is a better evaluation technique than NPV in a situation of capital rationing. For example two projects may have the same NPV of Rs. 10,000 but Project A requires initial outlay of Rs. 1,00,000 whereas B only Rs. 50,000. Project B would be preferred as per the yard stick of PI method.
6. Discounted Payback Period Method:
In this method the cash flows involved in a project are discounted back to present value terms as discussed above.
The cash inflows are then directly compared to the original investment in order to identify the period taken to payback the original investment in present values terms.
This method overcomes one of the main objections to the original payback method, in that it now fully allows for the timing of the cash flows, but it still does not take into account those cash flows which occur subsequent to the payback period and which may be substantial.
The method is a variation of payback period method, which can be used if DCF methods are employed.
This is calculated in much the same way as the payback, except that the cash flows accumulated are the base year value cash flows which have been discounted at the discount rate used in the NPV method (i.e., the required return on investment).
In addition to the recovery of cash investment, the cost of financing the investment during the time that part of the investment remains unrecovered is also provided for.
It thus, unlike the ordinary payback method, ensures the achievement of at least the minimum required return, as long as nothing untoward happens after the payback period.
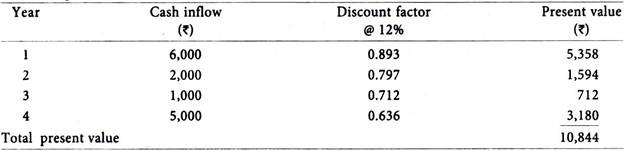
Illustration 6:
Geeta Ltd. is implementing a project with an initial capital outlay of Rs 7,600. Its cash inflows are as follows:
The expected rate of return on the capital invested is 12% p.a. Calculate the discount payback period of the project.
Solution:
Computation of Present Value of Cash Flow
Analysis – The discounted payback period of the project is 3 years i.e., the discounted cash inflows for the first three years (i.e., Rs. 5,358 + Rs. 1,594 + Rs 712) is equivalent to the initial capital outlay of Rs. 7,600.
7. Terminal Value Method:
Under this method it is assumed that each cash flow is reinvested in another project at a predetermined rate of interest.
It is also assumed that each cash inflow is reinvested elsewhere immediately until the termination of the project.
If the present value of the sum total of the compounded reinvested cash flows is greater than the present value of the outflows the proposed project is accepted otherwise not.
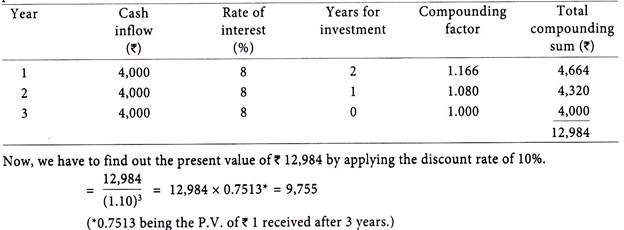
Illustration 7:
Original outlay Rs. 8,000
Cash inflows Rs. 4,000 p.a. for 3 years
Life of the project 3 years
Cost of capital 10% p.a.
Expected interest rates at which the cash inflows will be reinvested:
First of all, it is necessary to find out the total compound sum which will be discounted back to the present value.
Here, since the present value of reinvested cash flow i.e., Rs. 9,755 is greater than the original cash outlay of Rs. 8,000, the project would be accepted under the terminal value criterion.