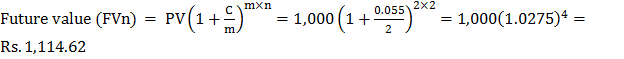The following article will guide to learn how to calculate annuity of cash flows in a company.
An annuity is a cash flow, either income or outgoings, involving the same sum in each period. An annuity is the payment or receipt of equal cash flows per period for a specified amount of time. For example, when a company set aside a fixed sum each year to meet a future obligation, it is using annuity. The time period between two successive payments is called ‘payment period’ or ‘rent period’.
The word ‘annuity’ is broader in sense, which includes payments which can be annual, semiannual, quarterly or any other fixed length of time. Annuity does not necessarily mean payment taken to be one year.
Future Value of Ordinary Annuity:
An ordinary annuity is one in which the payments or receipts occur at the end of each period. In a five year ordinary annuity, the last payment is made at the end of the fifth year.
Where, A = Annual or future value which is the sum of the compound amounts of all payments.
P = Amount of each instalment
i = Interest rate per period
n = Number of periods
Problem 1:
Mr. X is depositing Rs.2,000 in a recurring bank deposit which pays 9% p.a. compounded interest. How much amount Mr. X will get at the end of 5th year.
Solution:
Problem 2:
Find the future value of ordinary annuity Rs.4,000 each six months for 15 years at 5% p.a. compounded semi-annually.
Solution:
Where, P = Rs. 4,000
i = 0.05/2 = 0.025
n = 15 x 2 =30
Let x = (1.025)30
Log x = 30 log 1.025 = 30x 0.0107 = 0.321
x = antilog 0.321 = 2.094
Problem 3:
Calculate the future value of Rs.1,000 invested in State Bank Cash Certificate scheme for 2 years @ 5.5% p.a., compounded semi-annually.
Solution:
Present Value of Ordinary Annuity:
The present value of an ordinary annuity is the sum of the present value of a series of equal periodic payments.
Where, V = Present value of annuity
Problem 4:
Mr. Y is depositing Rs.8,000 annually for 4 years, in a post office savings bank account at an interest of 5% p.a. Find the present value of annuity.
Solution:
P = Rs. 8,000 i = 0.05 n = 4
Let:
x = (1.05) -4
Log x = -4 log 1.05 = -4 x 0.0212 = -0.0848
= -1 + 1 – 0.0848 = 1̅.9152
x = antilog (1̅.9152) = 0.8226
V = 1,60,000 x (1 -0.8226) = 1,60,000 x .1774 = Rs.28,384
Present Value of Deferred Annuity:
An annuity where the first payment is delayed beyond one year, the annuity is called a ‘deferred annuity’.
The present value ‘V’ of a deferred annuity ‘P’ to begin at the end of ‘m’ years and to continue for ‘n’ years is given by:
Calculation of present value by applying the above formula would be extremely tedious. The simple way of calculation is presented in the following illustration.
Problem 5:
Z Ltd. intend to invest Rs.15,000 per annum at the end of years 5,6,7 and 8 at an annual interest rate of 12%. Find out the present value of the deferred annuity payments.
Solution:
Present Value of Perpetuity:
A perpetuity is a financial instrument that promises to pay an equal cash flow per period forever, that is, an infinite series of payments and principal amount never be repaid.
The present value of perpetuity is calculated with the following formula:
Problem 6:
X Ltd. had taken a freehold land for an annual rent of Rs.1,200. Find out the present value of freehold land which is enjoyable in perpetuity if the interest rate is 8% p.a.
