The following article will guide you to learn about how to calculate standard deviation and coefficient of variation.
Standard deviation is a statistical technique used in capital budgeting decisions to determine the variation or deviation from the mean of cash flows of the project.
The project with lesser standard deviation in cash flows carries less risk and uncertainty.
Risk is measured by the possible variation of outcomes around the expected value. The capital investment decision will be taken keeping in view the variation in the expected value where two projects have the same expected value.
The decision maker will choose the project which has smaller variation in expected value.
In case if the life of the project and initial cash outflow of the two projects are similar, then standard deviation of both the projects can be used in selection of the project.
But when the life of the projects and their cash outflows differ, the selection of the project will be done by ascertaining the coefficient of variation instead of standard deviation.
The basic assumption is that probability distribution of cash flows is approximately normal.
When two projects may have similar EVs of profit, although not exactly the same.
In such circumstances, a useful measure of risk for project comparison is the coefficient of variation, which is calculated as follows:
A project with a higher coefficient of variation would be more risky than a project with a lower coefficient of variation.
Illustration:
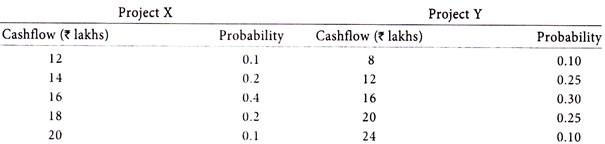
A company is considering taking up of one of two projects. ‘X’ and ‘Y’. Both projects have the same life, require equal investment of Rs. 80 lakhs each and both are estimated to have almost the same yield. As the company is new to this type of business, the cash flows arising from the projects cannot be estimated with certainty.
An attempt was, therefore, made to use probability to analyze the pattern of cash flow from either project during the first year of operation. This pattern is likely to continue during the life of these projects.
The results of the analysis are as follows:
Which project should the company take up? Show workings to justify your answer.
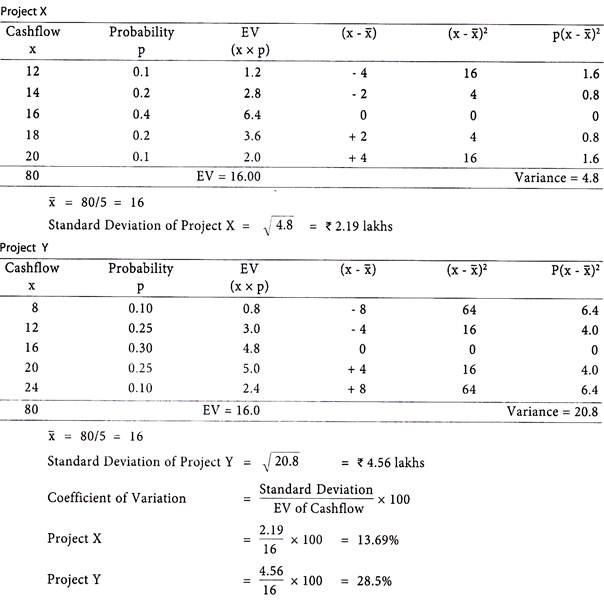
Solution:
Calculation of Standard Deviation.
Analysis – Project Y is more risky than Project X and the risk involved in it is more than double.