Following are some of the important methods which are used for equipment replacement studies: 1. Pay-Back Period Method 2. Total Life Average Method 3. Annual Cost Method 4. Present Worth Method 5. Rate of Return Method 6. M.A.P.I. Method.
1. Pay-Back Period Method:
This method of equipment replacement studies determines as to how long it will take (in years) to pay back invested capital.
Let,
P = Pay-back period in years.
ADVERTISEMENTS:
C = Original capital investment.
R = Annual return expected (i.e. total annual earning after deducting taxes).
Then P = C/R
This method is not much reliable as it does not take into account its insurance, interest and maintenance. Further, in the beginning the return is generally less, which increases gradually but here it is considered to be constant. This method does not consider depreciation and obsolescence.
2. Total Life Average Method:
ADVERTISEMENTS:
In this method of equipment replacement studies, all the costs involved in buying, operating and maintaining an equipment or asset are added together into one total figure and this sum is divided by the total estimated life to get an average annual cost.
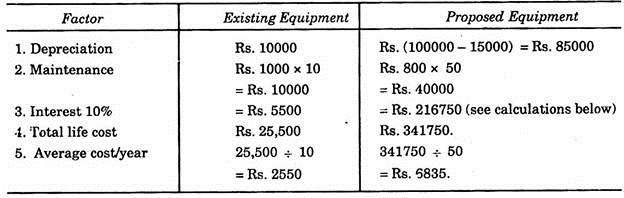
Example 1:
An existing piece of equipment has its market value of Rs.10,000, maintenance cost is Rs.1000 per year and has a life of 10 years and no salvage value. The interest rate is 10%. The proposed equipment has an installed cost of Rs.100,000, maintenance cost of Rs.800 per year, a life of 50 years and salvage value of Rs.15,000. Suggest, whether proposed equipment should be purchased or not.
Solution:
Interest is calculated by the following method:
Interest for existing equipment.
Total life = 10 years
Since average cost per year of existing equipment is much lower than the proposed equipment, hence new equipment should not be purchased.
3. Annual Cost Method:
This method of equipment replacement studies is to compare the annual costs of obtaining service from different equipment’s.
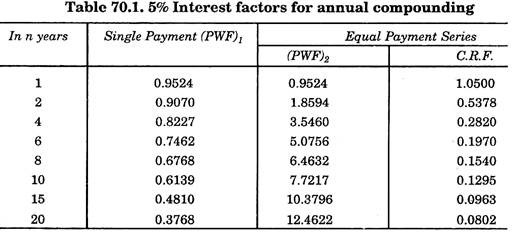
The following table gives the values of C.R.F. at different values of annual compound interest:
Tables for other values of rate of interest for different values of machine life in years are also available.
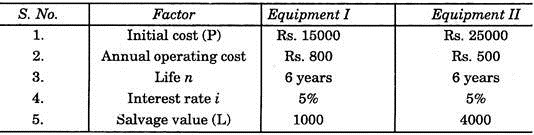
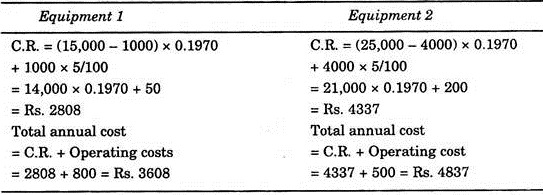
Example 2:
The cost details of two equipment’s are given below, find out the most economical one:
Capital Recovery C.R = (P-L) x C.R.F. + L x i
ADVERTISEMENTS:
The value of C.R.F. for i = 5% and n = 6 years can be seen from tables which is 0.1970.
Total annual cost of equipment 1 id less, therefore, equipment 1 should be chosen.
ADVERTISEMENTS:
Example 3:
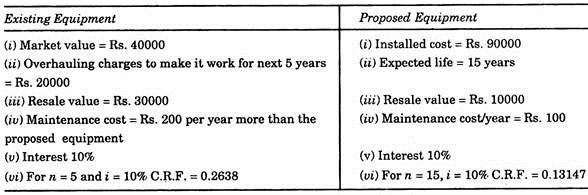
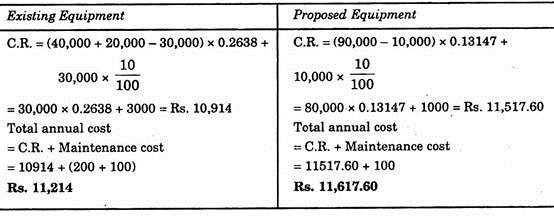
The following are the data for two equipment’s, suggest whether to purchase the equipment or not:
Solution:
As existing equipment involves lower total annual cost, the proposed equipment should not be purchased.
4. Present Worth Method:
ADVERTISEMENTS:
This method of equipment replacement studies is accurate and reasonable and used to evaluate the present value of new equipment. For the purpose of comparison, future costs are translated into today’s value of money.
A “present worth of rupee” is today’s value of money invested (at certain interest rate) after given number of years from today.
This can be clearly understood by the following examples:
If we have Rs.5000 to invest and want to know what will be its worth in 10 years at 10% interest, using the formula
F = p (1 + i) …(1)
where
ADVERTISEMENTS:
F = Worth of money in future,
P = Present amount of money
i = Interest rate and
n = Number of years.
Substituting in equation (1), we have, F= 5000 (1 + 0.10)10 = 5000 (2.594) = Rs.12,970.
Thus Rs.5000 today is worth Rs.12,970 after 10 years from now or in other words Rs.12,970 after 10 years from now has a present worth of Rs.5000.
ADVERTISEMENTS:
While comparing two alternatives all the costs must be translated into present worth and they must be compared for equal length of services e.g. if machine A has life of 3 years and B has 6 years then to compare the two machines we must compare the present worth value of 6 years’ service of two A machines and one B machine.
In equation (1), (1 + i)n is called “compound amount factor”. The values of (1 + i)n can be seen from tables for equal payment series, Present Worth Factor (P.W.F.) can be calculated by putting the values of n and i in equation (1).
Similarly, we can solve for P, to determine the present worth of a sum to be paid in n years hence that is
where, 1/(1=0.10)10 = Present value of a single payment F to be made in n years with interest i.
Therefore, if we were to receive a payment of Rs.10,000 in 10 years, we should be willing to accept a smaller but equivalent sum now. If interest at the rate of 10% is charged then smaller but equivalent sum would be
ADVERTISEMENTS:
P = 10,000 × 0,3855 = Rs.3855
Since1/(1=0.10)10 = 0.3855 is known as single payment present worth factor (P.W.F.)
The value of (PWF) can be seen from the tables or can be calculated by the above formula.
The present-worth method of evaluation is very popular because future expenditures or receipts are transformed into equivalent rupees now. That is, all the future cash flows associated with an alternative are converted into present rupees. In this form, it is very easy to see the economic advantage of one alternative over another.
The comparison of alternatives having equal lives by the present-worth method is straight forward. If both alternatives are used in identical capacities for the same time period, they are termed equal-service alternatives.
When the present-worth method is used for comparing mutually exclusive alternatives that have different lives, the alternatives must be compared over the same number of years. A fair comparison can be made only when the present worth’s represents costs and receipts associated with equal service as described earlier. Failure to compare equal service will always favour the shorter lived alternative, even if it were not the most economical.
ADVERTISEMENTS:
The equal service requirement can be satisfied by comparing the alternatives over a period of time equal to the least common multiple (LCM) for their lives. For example, if it is desired to compare alternatives which have lives of 3 years and 2 years, respectively, the alternatives are evaluated over a period of 6 years.
Example 4:
Initial cost of an equipment is Rs.10,000, annual operating cost is Rs.1000 and life of equipment is 8 years. If the salvage value is 1000 and interest rate is 5%.
Find the present worth of the equipment:
PWF2 for n = 8 and i = 5% is 6.4632
PWF1 for n = 8 and i = 5% is 0.6768.
Solution:
Initial cost = Rs.10,000.
Present worth of annual Operating cost = 1,000 × (PWF)2 (for 8-years and i = 5%).
= 1,000 × 6.4632 = Rs.6463.20
Present worth of salvage value = 1,000 x (PWF)1 for 8 years and i = 5%
= 1000 × 0.6768 = Rs.676.8
... Present worth of equipment = 10,000 + 6463.20 – 676.80 = Rs.15,786.40 Ans.
The net total Rs.15,786.40 is the present value of the expenditure over the 8 years expected life of the equipment. The initial investment is already at present value, i.e., the present value factor (PFW)2 is 1.00. The annual costs of operation are on 8 year annuity, so the entire stream of annual costs can be adjusted to present value by the multiplication of (PFW)2. Finally the present value of salvage is deducted.
Example 5:
Describe the present-worth for the purpose of depreciation.
A machine costing Rs.10,000 has yearly operating charges of Rs.200. If it has a 10 year life and money is worth 6%, what is the present worth of the cost for service provided by the machine? Given that (SPWF – 6% – 10) = 7.2965.
Solution:
(i) Initial cost of machine = Rs.10,000.
(ii) Present worth of operating charges = Rs.200 × (PWF)2 (for 10 years and i = 6%
= Rs.200 × 7.2965 = 1459.30
Total present worth of machine = Rs.10,000 + Rs.1459.30 = Rs.11,459.30 Ans.
Example 6:
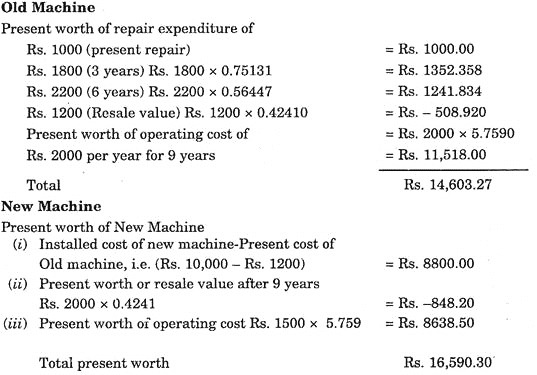
A manufacturing firm has an old machine, which is overhauled after every 3 years, can give service upto a total period of 9 years. Assuming the expenditure data given below, suggest whether new machine which also has a life of 9 years should be purchased or not.
Old Machine:
1. Cost of present repair = Rs.1000.
2. Cost of repair after 3 years = Rs.1800.
3. Cost of repair after next 3 years = Rs.2200.
4. Resale value after 9 years = Rs.1200.
5. Operating costs = Rs.2000/year for 9 years.
6. Old machine at present can be sold for Rs.1200.
New Machine:
1. Installed cost = Rs.10,000.
2. Resale value after 9 years = Rs.2000
3. Operating costs Rs.1500/year for 9 years.
Assume interest @ 10%
Given that for i = 10% and
n = 3, single payment present worth factor = 0.75131
n = 6, S.P.P.W.F. = 0.56447
n = 9, S.P.P.W.F. = 0,42410
and equal payment series present worth factor
for i = 10% and n = 9 years is 5.7590.
Solution:
As the present worth of old machine is less than present worth of new machine, therefore, new machine should not be purchased.
Example 7:
Machine A, operated manually costs Rs.2000, has a life of 2 years. While an automatic machine B costs Rs.3000 but has a life of 4 years. Operating cost for machine A is Rs.4000 per year, while that of machine B is Rs.3000 only. Which of the machines should be purchased? Consider 10% interest.
Solution:
For comparing the two machines for equal period we must consider two machines A against one machine B. Expenses of each is to be converted into present worth.
Total expenditure on machine B in terms of present worth = Rs.12,509
Thus the machine B is economical as its expenses are less and hence machine B must be purchased.
Example 8:
A company is considering to purchase a machine for a job. Two alternative machines are available in the market- one a standard machine and the other a semi-automatic one.
The comparative data of them are given below:
All the costs incurred during a year can be assumed to occur at the end of the year. The prevailing interest rate for money is 10% using the present value method, determine which machine is to be preferred.
Solution:
Example 9:
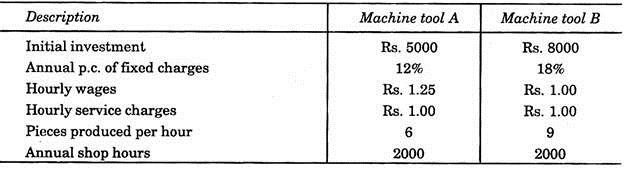
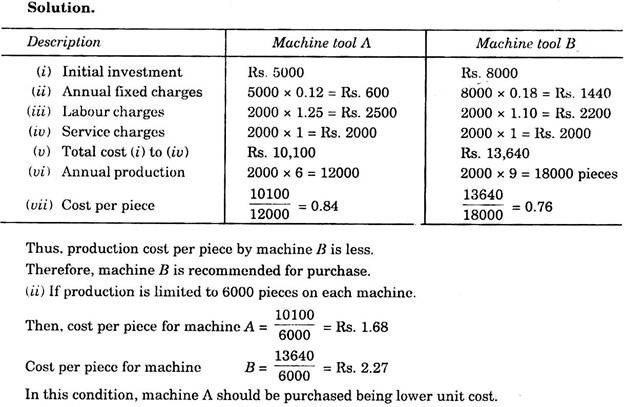
For a specific work, two machine tools are available in the market with the following operating data:
(i) If both the machines are assumed to be operating continuously throughout the year, which of the machine tools should you recommend for purchase, basing your decision on the “lower cost per unit of output”?
(ii) If both the machines cannot be used on any other kind of work and the annual production is limited to 6,000 parts, instead, which of the two machine tools shall provide lower cost per piece?
Example 10:
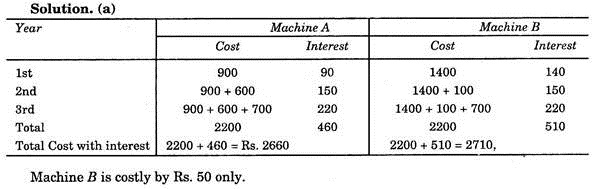
(a) Cost patterns for two machines A and B are shown below.
(Cost in rupee at beginning of the year)
If cost of money is 10%, which machine is costly and by how much?
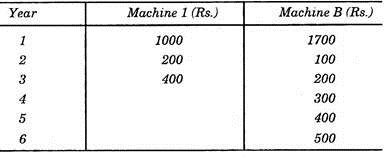
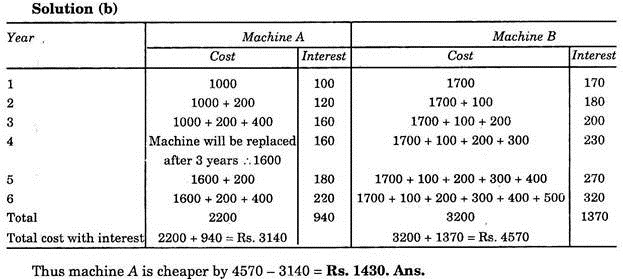
(b) Yearly outlays for machine, 1, which is to be replaced every 3 years and for machine 2, which is to be replaced every 6 years are given below:
If cost of money is 10% which machine is advantageous and by how much?
Example 11:
Machine A, operated manually, costs Rs.4000 has a life of 2 years. While an automatic machine B costs Rs.5000 but has a life of 4years. Operating costs for machine A is Rs.4000 per year while of machine B is Rs.3000 only. Which should be purchased? Consider 10% interest.
Solution:
For comparing the two machines for equal period we must consider 2 machines A against one machine B. Each of the expense is to be converted into present worth.
Thus the machine B is economical as its expenses are less and hence machine B must be purchased.
5. Rate of Return Method:
In this method average annual net income (after tax and depreciation deductions) is expressed as percentage of capital investment.
The formula used for this purpose is:
Percentage rate of return Earnings per year/Net investment × 100
For example a new equipment with net investment of Rs.20,000 gives an average earning of Rs.4000 per annum after deducting taxes and depreciation, then
Percentage rate of return = 4000 × 100/2000 = 20%
But this method has a drawback that earnings of all the years cannot have the value equal to that of today (present worth). Hence the method will be more useful and practical if the earnings of all years are first converted to present worth and then calculations are made for rate of return. Following method is an improvement over this method.
Discounted Rate of Return:
In this case following formula is used:
Example 12:
Whether a machine having following particulars must be purchased or not:
Now the question is whether this 21% return is high enough to justify the investment. If the rate of interest is 10% this return of 21% on the investment is worthwhile and the machine can be purchased.
6. MAPI Method:
The term MAPI stands for Machinery and Allied Products Institute of Washington, who has developed this method. This IS a method developed by George Terborgh, the Director of this institute.
The method is described as follows:
Almost all the equipment’s are subjected to deterioration and obsolescence in varying degree with the passage of time. Thus with the passage of time operating inferiority increases. Hence the old machine has his operating inferiority high and book value as low.
While a new machine will have operating inferiority minimum and cost, at a minimum. Hence the problem before manager is to choose between more capital cost and less imperfection, on one hand and less capital cost and more imperfection, on the other.
The MAPI has developed a new approach which helps in deciding this problem. The existing equipment which is to be replaced is known as DEFENDER and the new which will replace the old one is known as the CHALLENGER.
For estimating as to whether the proposed replacement is profitable, the “adverse minimum” of the defender and the challenger are found and compared. “Adverse minimum” of the defender or the challenger is the lowest sum of the time adjusted average of capital cost and operating inferiority (expressed in terms of money) obtainable from a machine. The calculations can easily be done with the help of MAPI charts.
Advantage of MAPI Method:
Following are some of the advantages of MAPI method:
1. Calculations are simple.
2. Management knows as to when a machine is to be replaced.
3. This method can be applied to a single as well as a combination of several machines for replacement.
4. It aids in budgeting equipment expenditure.
5. There is full provision for future deterioration and obsolescence on the new machines.