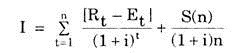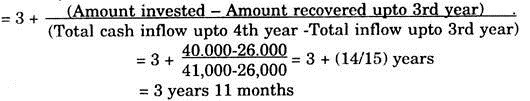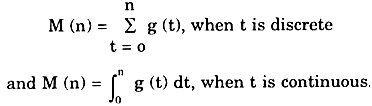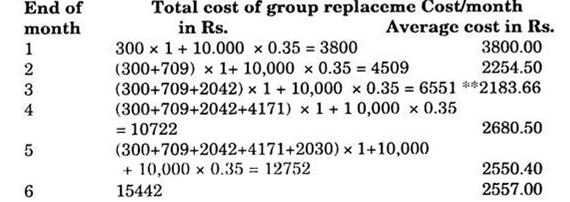In this article we will discuss about:- 1. Introduction to Capital Investments of an Organisation 2. Present Value Concept 3. The Loss Value of a Plant 4. Various Methods for Comparing Investment and Replacement Alternatives 5. Replacement Analysis.
Contents:
- Introduction to Capital Investments of an Organisation
- Present Value Concept
- The Loss Value of a Plant
- Various Methods for Comparing Investment and Replacement Alternatives
- Replacement Analysis
1. Introduction to Capital Investments of an Organisation:
Every organisation big or small has to invest huge capital for installation of the plant as well as during the process of manufacturing the product. The decisions regarding capital expenditures have far reaching consequences on the performance of the enterprise e.g. capital hired/acquired on long term credit creates a continuing liability to the organisation.
ADVERTISEMENTS:
Capital investments can be divided into three main categories:
(i) Investment on Fixed Assets:
Basically these are the expenditures on men, material and machine/equipment required for manufacturing. The planning of this expenditure is to be done either before the installation of the plant or before the start of actual production. One important feature of such expenditures is that once acquired, the capital assets cannot be disposed of without any loss.
Similarly if an additional asset does not adequately increase the earnings, then these may adversely affect the financial obligations of the enterprise. It is observed that for producing same type of item the organisation can use varying amounts and kinds of input i.e. man, machine and material. Thus there are a number of alternatives in which the capital expenditure can be made.
(ii) Expenditures During Course of Production:
ADVERTISEMENTS:
This is also known as cost of production. It is a running expenditure and its magnitude depends on the nature of inputs. Wrong capital investment and misuse may result in increasing operating costs and proportionate decrease in return on investments. Thus balancing expenditures against expected saving in future operating costs need proper analysis of various financial aspects of the operations of an enterprise. This expenditure can also be done in a number of alternative ways.
(iii) Replacement Expenses:
It is a natural phenomenon that in every system the efficiency of various factors of production deteriorates with time or sometimes the item fails completely, thus adversely affecting the whole system.
In such cases either the item is to be replaced completely or there is a need of some remedial measure, i.e. maintenance, to restore the level of efficiency at the desired level. Replacement investments may be desired due to incretions in production technology i.e. for the modernization of the system.
The capital expenditure may also relate to:
ADVERTISEMENTS:
(a) Cost reduction by:
(i) Replacement of machinery and equipment
(ii) Plant rearrangement programme or mechanisation of the process.
(b) Providing facilities to manufacture components, which are currently purchased.
ADVERTISEMENTS:
(c) Installation of new plant and machinery for taking up a new product on product lines.
In view of many uncertainties, scientific and systematic planning and control of capital expenditure is of great significance in modern management.
The process of capital expenditure involves planning the availability and controlling the allocation and expenditure of long-term investment funds by determining:
(i) How much money is needed for the capital expenditure in future?
ADVERTISEMENTS:
(ii) How much money will be available for investment?
(iii) How the funds available will be allocated to the projects under consideration?
The most common feature of all these expenditures is that there are a number of alternative ways to plan these expenditures to get the desired result and every organisation wants to formulate an investment policy which is most efficient and economic to the organisation as a whole. Thus the Economy study of production management is a procedure to select the most profitable investment or replacement strategy.
2. Present Value Concept:
ADVERTISEMENTS:
Every expenditure made today has some opportunity cost associated with it i.e. there will be some return available on it depending upon the period of return. Alternately, whenever some expenditures are made, then the arrangement for these is done either by borrowing from some agencies and paying interest on that or paying it from one’s savings which otherwise could have fetched some interest.
Thus in each case some return in monetary terms is associated with each investment. This return depends on the amount of investment as well as the period for which the money is to be invested. The money borrowed or invested from savings is known as Principal and the money paid as interest or loss of return on savings due to investment is known as interest.
The sum of Principal (P) and Interest (I) is known as amount (A).
Mathematically, the relationship between the three can be written as:
Thus the present value of a sum to be spent within a given period depends on the rate of interest and the period within which the amount is to be repaid.
There are two ways of paying interest:
(a) Simple interest and
(b) Compound interest.
(a) Simple Interest:
It is amount paid yearly (or some other specified period) on the principal amount e.g. if an amount P is borrowed at a fixed interest rate r per rupee per year, then in one year the interest will be i.P. next year also the interest will be iP: and in rth year again the interest will be iP. So if total investment is to be paid back in r years, then the total interest paid in r years will be,
l = iP + iP + … iP rtimes
ADVERTISEMENTS:
= riP ….(9.2)
Thus putting the value of I from (9.2) in (9.1), we get
A = P + riP
= P (1 + ri) ….(9.3)
Note: Generally interest rate is specified in percentage i.e. t% per year.
In that case, r = t/100 per year ….. (9.4)
ADVERTISEMENTS:
It is evident from (9.3), that the amount A increases progressively in arithmetic progression.
(b) Compound Interest:
In this case, the whole amount A is to be paid at the end of the period.
Here every year the interest accrued is also added to the Principal of previous year to get the new principal for, next year i.e. at the end of first year the new principal will be:
P1 = P + iP = P(1 + i)
at the end of second year the principal will be
P2 = P1 + iP1 = P1 (1+ i)
ADVERTISEMENTS:
P(1 + i) (1 + i) = P( 1 + i)2
and at the end of r th year-the principal will become
A = Pr – l + iPr – 1 = Pr – 1(1 + i)
= P(1 + i)r-1 (1 + i) = P(1+ i)r …..(9.5)
or A = P (CAF) …..(9.6)
where CAF known as compound amount factor is (1 + i)r
ADVERTISEMENTS:
From (9.5), we get
P = A/(1 + i)r = A (PWF) …..(9.7)
where PWF = 1/(1 + i)r is known as present worth factor.
There are standard tables of CAF and PWF for different values of i and r. The values of P or A can be immediately determined with the help of these tables. The method is illustrated by the following examples.
Example 1:
Find the amount paid in 10 years for a Principal of Rs. 1000 at (i) simple interest of 10% and (ii) compound interest of 10% per year.
ADVERTISEMENTS:
Solution:
Here t = 10% i.e. i = t/100 = 10/100 = 0.1 per year, r = 10
(i) From (9.3) A = P (1 + ri)
= 1000 (1 + 10 × 0.1) = Rs. 2000/-
(ii) Now from (9.6)
A = P (CAF)
Here, P = Rs. 1000 and CAF at the rate of 10% in 10 yrs
= 2.594
Thus, A = 1 000 (2.594) = Rs. 2594/-
Example 2:
If the amount paid after 5 years is Rs. 5000/-, then find the Principal at (i) simple interest rate of 5%, (ii) compound interest of 5%.
Solution, (i) Here I = 5/100 = 0.05, A = Rs. 5000, r = 5 years and we want to find P
From (9.3), A = P (1 + ri)
i.e. 5000 = P [1 + 5(0.05)] = P[1.25]
P = (5000/1.25) = Rs.4000
(ii) From (9.7), P = A (PWF)
(for 1 = 5% and r = 5, PWF = 0.7835)
= 5000 × 0.7835
= Rs. 3917.50
(iii) There are some situations, where the borrower agrees to repay some fixed amount at fixed intervals of time i.e. the money is repaid in fixed installments. If the total amount A accrued in r years is paid in r, installments of Rs. K, then
A = K [(1 + i)r – 1]/I = K(CAFS), …..(9.8)
where CAFS = [(1 + i)r -1 ]/i is known as uniform annual series compound amount factor,
Now, knowing A, we can write:
3. The Loss Value of a Plant:
The plant installed today start immediately to loose its value due to two main reasons namely, Depreciation and Obsolescence.
Depreciation:
The production capacity introduced by some Capital investment tends to decline with time. There is also diminution in the intrinsic value of an asset due to use as well as with passage of time. This diminution may also be due to bad handling, poor maintenance, accidents etc. This decline in the value of investment is known as Depreciation.
Depreciation rate can be calculated in two ways:
(i) Straight Line Method:
Here we assume that there is a constant, rate of decline during an asset’s life. Thus same absolute value is deducted from the value of the assets for each period of use.
i.e. value = P – P(n – 1)/N
where n is the year at which the value is to be calculated and N is the total life of the assets. Alternately the depreciation rate can also be calculated by the formula
where D: annual depreciation rate
D = F – S/N
F: investment cost
S: estimated salvage value
N: estimated life of investment.
(ii) Declining Balance Method:
Here some constant percentage from book value is deducted.
Thus value of the asset after n years can be
Value = P (1-R)n – 1
where R is the depreciation rate.
Alternately
D = Fixed Percentage x F/N
Obsolescence:
Loss in the intrinsic value of an asset due to its: suppression which is the outcome of reduction in the market demand of the product manufactured by the plant or change in the design of the plant etc. is known as obsolescence. This may lead to formulation of suitable replacement policy.
4. Various Methods for Comparing Investment Alternatives
:
In planning any production strategy one very often faces a situation when decisions on investment and replacement proposals are to be taken. There are a number of alternatives, each involving huge capital expenditure, Evidently for making an appropriate decision an economic analysis is more useful for differentiating between various alternatives.
The basic steps involved for critical appraisal of various alternatives are:
(i) To evaluate the cost of products and other investment requirements i.e. how much money is needed for desired expenditure during the period under consideration.
(ii) Determination of anticipated returns and life of the invested capital.
(iii) Timing of the investment in relation to anticipated requirements.
(iv) How much money can be made available for the purpose and what will be the sources and expenditure for these funds? The funds can be generated in different ways.
Some of these can be:
(a) Hire-Purchase:
Contracts can be negotiated for long periods with the interest tied to the bank rate. In some cases payments can fluctuate with known seasonal variation in output.
(b) Leasing:
Here the user never accurately owns the equipment leased. The use of the plant is considered to be more important than its ownership.
(c) Hiring:
In fact this is some sort of leasing but in it a maintenance contract is also implied or required.
Various methods to compare alternative proposals can be divided into two main categories:
1. Present Value Approach:
(a) Present Value Basis:
Under this method, investment decisions are based on the amount by which the present value of a projected income stream exceeds the cost of an investment. Here both the streams of inflows and outflows are discounted at a calculated rate. The basic assumption behind all discounting is that the cash inflows are re-invested at the discounting rate in net projects as soon as they arise.
Thus in this approach present values of all future expenditures and revenues are calculated for various alternatives and the Net present value of total cost is compared. The alternative with minimum net present value is considered to be most appropriate.
Case (i) In the Absence of any Annual Income:
If there is an initial investment of P rupees with a recurring expenditure of K rupees per year for r years and at the end of r years the salvage value is S, then the present value of total cost is given by
P + K Pwfs – SPwf …(9.12)
where Pwfs and Pwf can be calculated at the given interest rate for a period of r years.
The procedure is explained by the following example:
Example 3:
An entrepreneur is planning to install a small machine in his factory.
The relevant data about the two alternative machines are as under:
As financial advisor of the company you have been asked to select the best machine, considering normal rate of return to be 12% per year.
(Pwf-series at 12% for 1 0 years = 5.650 Pwf single payment at 12% for 10 years = 0.332).
Solution:
Here we should calculate the present value of total cost Incurred on each of the machines In 10 years by using (9.12).
For Machine A,
P = 1,00,000, K = 20,000, S = 5000, Pwfs = 5.65 and Pwf = .332
Present value of total cost = P + K Pwfs – SPwf
= 1,00,000 + 20,000 (5.650)-5000 (0.322)
= 1,00,000 +1,13,000-1610
= 2,13,000 – 1610
= Rs. 2, 11,390
For Machine B,
P = 1,50,000, K = 12,000 and 5 = 2,000
Present value of total cost
= 1,50,000 + 12000 (5.650) – 2000 (0.322)
= 1,50,000 + 6,78,00-644
= 2,17,800 – 644
= Rs. 2,17,156
Evidently, present value of total cost for Machine A is lesser than that for Machine B.
Hence the company should select machine A.
Case (ii). There is some Fixed Annual Income from the Investment, say Every Year. Then the Present Value of this Annual Income for the given Period can be Calculated by using Pwfs.
Then the present value of net income
= Present value of Total Revenue – Present value of total cost
The alternative for which present value of net income is maximum is considered to be most appropriate.
Alternately, calculate present value index for each alternative, and the alternative for which present value index is maximum is considered to be the best.
Present value index is given by:
PVI = Present value of future income/initial investment …..(9.13)
or PVI = Present value of annual income/Present value of total cost
Present value index provide some valuable information about the investment policy i.e.
If P. V.I. < 1 return is less than normal interest on investment
= 1 break even situation
> 1 return is more than normal interest on investment
The method is illustrated by the following examples:
Example 4:
To start a business it needs an investment of Rs. 50,000. The income in next 25 years is expected to be Rs. 8,000/- per year with an expenditure of Rs. 3,000 per year. The value of the establishment at the end of ’25 years is expected to be Rs. 18,000. If minimum interest rate is 10% then would you recommend the investment?
(Pwfs – 10% – 25) = 9.077, (Pwf- 10%-25) = 0.0923.
Solution:
Here P = Rs. 50,000
K = As. 3000 per year
r = 25 years I = 10%
R = Rs. 8000 per year.
Now from (9.12) Present value of total cost
= Rs. 50,000 + 3000 (9.077) – 18000 (0.0923)
= Rs. 50,000 + 27231 – 1661.40
= Rs. 77231 – 1661.40
= Rs. 75569.60.
Present value of total income = Rs. 8000 x 9.077
= Rs. 72616.
Now present value of total income is less than the present value of total cost. Thus it is not advisable to recommend the investment.
Aliter:
Present value index = Present value of future income/Present investment
Now present value of future income
= (income per year) Pwfs + (value of the establishment at the end of 25 years) Pwf – Annual expenditure (Pwfs)
= (8000 x 9.077) + 18000 (0.0923) – (3000 x 9.077)
= Rs. 72616 + Rs. 1661.40 – Rs. 27231
= Rs. 74277.40 – Rs. 27231 = Rs. 47046.40
Hence PVI = 47046.40 = 0.94/50,000
Since PVI < 1, the project is not to be recommended for investment.
Example 5:
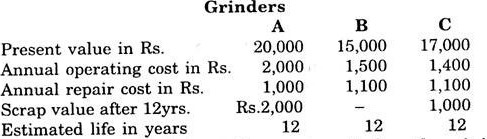
A company is considering to purchase a new grinder.
The cost data of alternative grinders are as follows:
Recommend the grinder to be purchased when the minimum rate of return is 8%.
Solution:
Total annual expenditure on each grinder can be calculated by Annual operating cost + Annual repair costs. Thus for the three grinders this cost will be Rs. 3000 for A, Rs. 2600 for 8 and Rs. 2500 for C. Now. present value of total cost for each grinder can be calculated from (9.12). It is
P.V = P + K (Pwfs – 8% – 12) – S (Pwf – 8% – 12)
Now for Grinder A
P.V. = 20000 + 3000 (7.536) – 2000 (0.3971)
= 20000 + 22608 – 794.20
= Rs. 41813.80
For Grinder B
= 15000 + 2600 (7.536) – 0 (0.3971)
= Rs.34593.60.
For Grinder C
P.V. = 17000 + 2500 (7.536) – 1 000 (0.3971)
= 17000 + 18840.00 – 397.10
= Rs. 35442.90
The present value of total cost is minimum for grinder B. Hence grinder B should be purchased.
Case (iii) Operating Costs Varying:
In practice running costs are never fixed. Actually these are found to be varying from period to period.
Suppose a machine’s expected life is r years, with running expenditures each year being R1 R2…Rr respectively. Now for the calculation of present value of these expenditures, we shall use Pwf with a period of one year for R1. two years for R2 and r years for Rr. Thus the present value of all running expenditures at an interest rate of t% per year will be given by the expression
R1(Pwf-t%-1 year) + R2 (Pwf-t%-2years) +…+ Rr (Pwf-t%-r years) …(9.14)
The net total cost can be determined in the usual manner.
The method is illustrated by the following example:
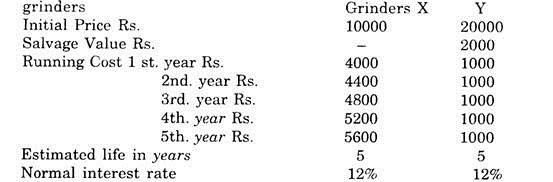
Example 6:
A company is considering to replace a grinder X presently of worth Rs. 10,000 by a new grinder Y of Rs. 20000 but will be economic in running expenditures. The expected life of grinder A is 5 years, with running expenditure of Rs. 4000 in first year and then an additional increase of Rs. 400 per year for next four years. For the new grinder annual running cost is Rs. 1000 per year and its scrap value is Rs. 2000.
As an advisor to the company, find:
(i) The present value of the cost of old and new grinders, considering 12% normal rate of return.
(ii) Suggest whether the old grinder be replaced by the new grinder summing the life of the new grinder to be 5 years.
Solution:
The following is the summary of costs associated with two:
(i) Present Value of Total Cost for X
= 1 0,000 + 4000 (PwI-12%-one year)
+ 4400 (PwF-12%-two years) + 4800 (PwF-12%-three years) + 5200(PwF-12%-four years) + 5600 (PwF-12%-five years)
= 10.000 + 4000 (0.8929) + 4400 (0.7972) + 4800 (0.7118) + 5200 (0.6355) + 5600 (0.5674)
= 10,000 + 3571.60 + 3507.68 + 3416.64 + 3304.60 + 3177.44
= 26977.96
Present Value of Total Cost for Y
= 20000 + 1000 (Pwfs -12% -5years) -2000 (Pwf 12% -5 years)
= 20,000 + 1000 (3.005) – 2000 (0.5674)
= 20,000 + 3005 -1134.80
= 20,000 + 1870.20
= Rs. 21,870.20
(ii) Evidently old grinder should be replaced by the new one.
(b) Annual Basis:
Here net annual cost is calculated for each alternative and the alternative for which this cost is minimum is considered to be the best, CRF and SFF are used for the given period.
Let P: Principal Value
S: Salvage Value
r: Estimated life in year
t: Normal rate of interest.
Case (i) Running expenditure annually be R.
Annual Capital Cost = P (CRF-t%-r years) -S (SFF-t%-r years) …(9.15)
Annual Running Cost = R
Total Annual Cost = Annual Capital Cost + Annual Running cost
Case (ii) With annual expenditure, there is also annual income from the investment.
Here we calculate
Annual Value Index = Annual income/Annual net total cost
Or Annual value of net total income/Annual value of present investment …(9.16)
Annual value of Net income = R (CRF- t%-r years) + S (SFF-t%-r years). The alternative with maximum annual value index is considered to be most appropriate.
The methods are illustrated by the following examples:
Example 7:
There are two investment alternatives A and B.
They are briefly described as follows:
The company feels that if invested elsewhere, its money would yield a return of 10% per year. Find which of the alternatives is more economical.
(CRF-1 0%-5) = 0.2638, (SFF-1 0%-5) = 0.1639
Solution:
In this example CRF and SFF are given. So comparison of the two alternatives can be done on annual basis only, using (9.15).
Alternative A:
Annual net total capital cost = (20000) (CRF – 10% – 5)
= 2000 (SFF – 1 0% – 5)
= 20000 (0.2638) – 2000 (.1639)
= Rs. 5276 – Rs. 327.80
= Rs. 4948.20
Net Annual Total Cost = Annual Capital Cost + Annual expenditure
= Rs. 4948.20 + Rs. 10000
= Rs. 14948.20
For alternative B:
Annual Capital Cost
= 30000 (CRF – 10% – 5) – 3500 (SFF – 10%:5)
= Rs. 7340.35
Net Annual Total Cost = Rs. 7340.35 + 8000
= Rs. 15340.35
Evidently alternative A is more economical.
(c) Last Basis:
In this case the value of all the expenditures and incomes is projected over the expected years to the last year. Thus the total cost of the project after r years is then given by
= P (CAF-t %-r years) + A (CAFS -t %-r years)-S …..(9.17)
The alternative for which Total cost is minimum is considered to be most appropriate.
The method is illustrated by the following example:
Example 8:
If you wish to have a minimum return of 10% per annum on your investment, which of the following plans would you prefer?
Solution:
Here we are given CAF and CAFS. So we should use the last basis approach to make a final decision.
Now for Plan A:
Total cost = 200,000(CAF-10%-15) – 1,50,000 = Rs. 6,85,400.
The annual income projected over 15 years
= 25000 (CAFS -1 0%-15)= Rs. 7,94,300
Thus net Profit in Plan A = Revenue – Cost
= Rs. 7,94,300 – Rs. 6,85,400 = Rs. 1,08,900
Similarly for Plan B the net profit will be Rs. 88,910.
It is observed that net profit for Plan A is more than for Plan B. Hence plan A is better than Plan B.
(d) Discounted Cash Flow Method:
This method is based on the concept that monies recovered over a period of time are not worth the same amounts at anyone point of time e.g. Re 1/- today and Re 1/- in a year time have quite different values today. Similarly a profit of Rs. 1000/- obtained in a stream of Rs. 200/- per year for 5 years has a different value to a stream of Rs. 100/- per year for 10 years.
The former is worth more than the later. Based on this principle an attempt is made to discount all income receivable at various points of time during the life of a given project. Similarly expenditure on a project also may be spread over a number of years and one may find its present worth.
Here discounting is the act of taking a sum in the future and calculating its present value, assuming some particular rate of return. Discounting can be considered inverse of compounding. The principle appears to be simple but in practice it is complicated to determine rate of return.
Mathematically, the discounted value is defined as:
Discounted value = X/(1+i)n
where X is the amount to be discounted, n is the period of discount and i is the interest rate.
There may be situations where annual earnings are not constant, investment is incremental and the lives of the investments are uneven.
In such case we can use the following formula:
where I : investment in Rs.
n: economic life in years
t: time variable
Rt: revenue for a given period.
Et: expenses for a given period.
S(n) = scrap value at the end of the economic life
i = discount rate.
2. Annual Cost Approach:
There are two main techniques in this approach, namely:
(a) Pay-back method
(b) Return on investment method.
(a) Pay-Back Method:
Whenever any investment is made some amount of return is always expected. Also it is hoped that the investment will be recovered within reasonable period of time. The period of recovery is of great significance for investment decisions.
It is commonly known as Pay-back period and is defined to be the period within which the initial investment, amount is recovered by net cash inflows. The rationale underlying the use of pay-back method is that the sooner the capital investment can be recovered, the sooner it can be reinvested in revenue producing projects.
In pay-back method, the period of recovery for each alternative investment strategy is calculated and then various alternatives are ranked in terms of recovery period viz, alternative with minimum recovery period is ranked first and so on. Pay-back period is the time required for each investment to return earnings equal to the cost of investment.
The method is based on the concept of net cash-inflows which is defined to be Net cash – inflow = [Cash-inflow from earnings – expenditure on operating costs’)
Note:
Expenditure on operating costs is known as cash outflow. It should include income tax on earnings but should exclude depreciation costs.
Now cash-inflow can be of two types:
(i) Even cash flow which is equal for different years and
(ii) un-even cash inflow which is not same for different years. In this case cumulative sum of cash inflows is calculated for each year.
The formula, for pay-back period is given by
Pay-back period = Amount Invested/Annual cash inflow …(9.18)
The method is illustrated by the following example:
Example 9:
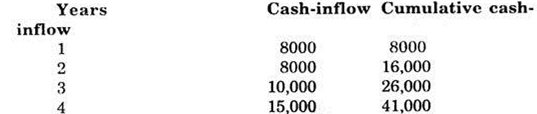
In an investment of Rs. 40,000 the organization expects (i) an even cash flow of Rs. 5000 per year and (ii) uneven cash-inflow of Rs.8000, Rs. 8000, Rs. 10,000 and Rs. 15,000 for first four years respectively.
Find the pay-back period in each case.
Case (i) From (9.18)
Amount invested/Annual cash-inflow = 40,000/5000 = 8 years
Case (ii) In the case of uneven cash-inflows, we calculate the cumulative cash-inflow year wise to know the year by which the investment amount is likely to be recovered.
The calculations can be done in the following tabular form:
It can be observed that upto 3rd year only Rs. 26,000 will be recovered. The balance of Rs. 14,000 will be recovered in fourth year. In this case Pay-back Period in years.
The following are the main drawbacks of pay-back method:
(i) Highly profitable projects do not necessarily pay-off in the initial years. Larger gains may occur later.
(ii) It completely ignores the time value of the money received during and after the pay-back period.
(iii) It does not measure the rate of return.
(b) Return on Investments Method:
Here profit is considered as return on investment. For various alternatives, profit is calculated after allowing for depreciation (but before taxation) expressed as a percentage of original investment. Mathematically
Percentage return on investment
= Average annual income after depreciation but before taxation / Original capital investment × 100
In this method allowance is made for decrease in the value of the asset due to wear and age and the cost of interest charged is spread uniformly over the projected life of the asset.
These methods may be classified as:
(i) Unadjusted rate of return method.
(ii) Time adjusted rate of return method.
(i) Unadjusted, Rate of Return Method:
The method is based on certain information’s extracted from various financial statements. Here future earnings on investment are not converted to get its present value that is why it is known as unadjusted return method. The rate of return on investment is calculated for each alternative and the one providing maximum return is considered to be the best. Unadjusted rate of return is given by
= Average Annual net income/Average investment x 100
= Average Annual cash – inflow – Annual depreciation/Average investment x 100 …(9.19)
Now average investment can be calculated by any of the methods given below, depending upon the nature of the information available.
(a) Average investment = (uncovered capital in the beginning + uncovered capital at the end)/2
(b) Average investment = (Initial investment + Scrap value)/2
(c) Average investment = [(capital recovered)/2] + Scrap value …(9.20)
(ii) Time Adjusted Rate of Return Method:
According to National Association of Accountants, America, “Time adjusted rate of return is the maximum rate of interest that could be paid for the capital employed over the life of an Investment without loss on the project.”
There are many other names of this method viz. Discounted rate of return method, internal rate of return method etc. This method is particularly useful when the rate of return on investments is not known exactly.
The method consists of following steps:
(a) Find the ratio of cost of investment and annual cash-in flow.
(b) For the value obtained in (a), find present value factor from Pwfs table for the given period.
In the case of uneven cash-inflows, trial and error method can-be used.
The method is illustrated by the following examples:
Example 10:
An investment of Rs. 12000 provides the annual cash inflows of Rs. 2000, Rs. 3000, Rs. 5000 and Rs. 6000 respectively in 1st, 2nd, 3rd and 4th years. Find Time adjusted rate of return.
Solution:
Here there is an uneven cash inflow. So we shall apply trial and error method to find Time adjusted rate of return.
First of all we find average annual cash-inflow
2000 + 3000 + 5000 + 6000/4 = 40000
Hence present value factor
= Investment/Average cash inflow = 12.000/4000 = 3.0
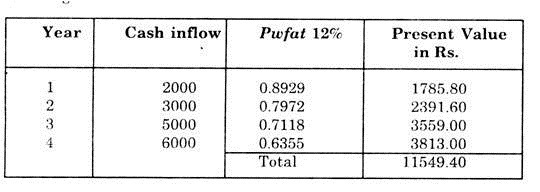
In Pwfs table, we find that in the row of fourth year, the value 3.0 lie in the column of 12%. Hence at first iteration the time-adjusted rate of return is found to be 12%. Now at this rate of return, we can calculate the present value of cash inflows for different years in the following tabular form
It can be seen that with rate of return to be 12% the total amount recovered in 4 years is Rs. 11549.40, which is less than the total investment of Rs. 12000. So the time adjusted rate of return should be somewhere between 12% and 13%.
The following are the drawbacks of rate of return method:
(i) It fails to give full effect to the time value of money, specially in cases where investments are made at different periods of time or when income from investments is not likely to accrue at a uniform rate.
(ii) The method does not recognize the true return on capital investments. In both these techniques no account is taken of the time at which the earnings are made.
5. Replacement Analysis:
The problem of replacement is an everyday phenomenon. It is experienced in systems where machines, individuals or capital assets are the main job performing units. It is a common phenomena that performance/efficiency of an item in a system deteriorates with time.
The remedy is either to replace the item with some new item or to restore the level of performance by some sort of maintenance.
Also, there comes a stage where maintenance of any item becomes so much expensive that it is more profitable to replace the item. Thus there is a necessity to formulate a most economic replacement policy, which is in the best interest of the system.
Them reasons for replacement are:
(i) Deterioration:
Decline in performance due to wear and tear indicated by increase in maintenance costs; reduction in product quality and rate of production, increase in labour costs, loss of operating time etc.
(ii) Obsolescence:
It may be due to advancement in technology. This reduces profits, impairs competition, causes loss in the value of machinery.
(iii) Inadequacy:
Equipment’s capacity may not be sufficient to meet the demand or it is not able to increase the production rate to desired level.
(iv) Working Conditions:
Causing unsafely to workers and leading to accidents, making the environment noisy and smoky etc.
(v) Economy:
The existing units have outlived their effective life and it is not economical to continue with them.
(vi) The existing units breakdown, perished or destroyed all of a sudden.
Some special characteristics of replacement are:
(a) Replacement reduces maintenance costs but it involves a high average capital cost.
(b) Many people feel that an equipment should not be replaced until it is physically Worn out. But this attitude is never in the interest of the organisation. On the contrary the equipment’s must be constantly reviewed and updated, otherwise these may become obsolete.
Replacement Models and their Solutions:
The study of replacement is some kind of application mostly concerning comparison of alternative replacement policies.
The various factors relevant to replacement analysis can be divided into two main categories; namely:
(i) Technical:
Deterioration, Obsolescence, Inadequacy.
(ii) Financial:
Initial cost; operating costs; labour costs, material costs maintenance costs, salvage value, insurance etc.
A well designed replacement policy should compare thoroughly an existing equipment with its possible replacement. In order to make a sound economic comparison strategy all the factors should be converted into costs.
The various types of replacement problems can be broadly classified in following situations:
I. Replacement of Items whose Efficiency Deteriorates with Time:
The simplest replacement model in such cases is one where the deterioration rate is predictable in terms of increasing maintenance costs and decrease in salvage value with time. The expenditure on replacement items is considered here as cost of replenishment in inventory, analysis and maintenance costs is like holding costs.
There are two methods to find appropriate solution in this case viz.
(a) Determination of cost per unit of time and
(b) Present value concept representing time value of money.
Under this situation the efficiency is measured as the discounted value of all future costs associated with each alternative e.g. the maintenance cost of a machine always increases with time and at some stage maintenance cost becomes so large that it is more economical to replace the machine by a new one. The criteria evolved such cases can be broadly divided in three categories namely,
Replacement of items whose maintenance cost increases with time, and
(a) the value of money remains same during the period
(b) the value of money changes with time.
Case (i) Replacement of items whose maintenance costs increases with time.
A. The Value of Money Remaining same During the Period:
Here we use the following notations:
C: Purchase price of the item.
S: Scrap value of item taken to be same over time.
g (t): Maintenance/running cost at time ‘t’:
Now g (t) can be discrete or continuous function of time. In the case of g (t) to be discrete we can use the summation sign to calculate the total maintenance cost in a given period otherwise integrals can be used e.g. in some given period ‘n’ the total maintenance cost will be
Thus the total cost incurred on the item in some period n is given by
Total cost = cost of the item + total maintenance cost in period ‘n’- scrap value.
= C + M (n)-S
Thus the average cost incurred per year on the item is given by
G (n) = C + M(n) – S/n
Now it is advisable to replace the item when G (n) is maximum. Without going into the mathematical treatment it can be seen that G (n) will be minimum when
g(n) < G(n-l)
and G (n) < g (n + 1)
So we get the following replacement criteria in this case. Do not replace the item if the next year maintenance cost is less than the average cost of the previous year and replace the item if next years average cost is less than the maintenance cost of next year i.e. when Average Cost is least.
The method is illustrated by the following examples:
Example 11:
The cost of a machine is Rs. 6100 and its scrap value is Rs.100.
The maintenance costs are found to be:
When should the machine be replaced?
Solution:
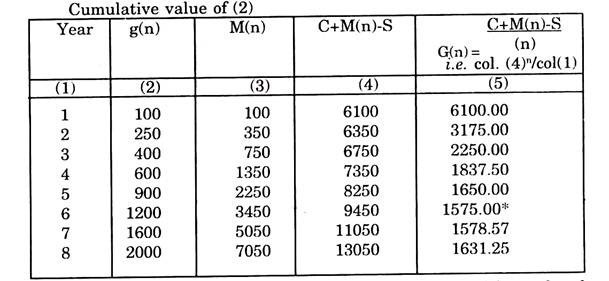
Here C= 6100. S = 100 and the maintenance costs are given at 11 discrete values of time.
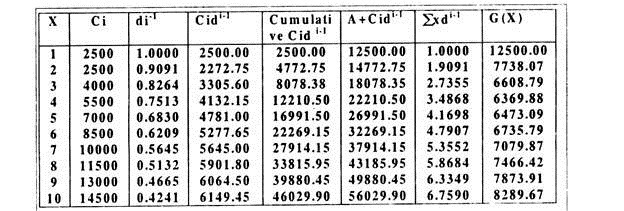
The total average costs in different years can be calculated in the following tabular form:
Average cost is minimum. Hence the machine should be replaced at the end of the sixth year.
B. The Value of Money Changes with Time:
There can be two situations in this case,
(a) The value of money decreases at a constant rate ‘d’. d is known as depreciation ratio or discounted factor. Here we want to find the optimum value of time at which the item should be replaced.
if d is the per unit depreciation rate, then the present value of one unit of money after a period of t years is given by 1/(1 + d)t.
(b) The manufacturer takes a loan at some given intrest and agrees to pay in a prescribed number of fixed installments. Then we want to find appropriate period of making in repayment of loan.
Case (a) Let the maintenance casts in X years be C1, C2…., Cx respectively, A, the purchase price of the item and ‘d’ be the per unit depreciation value. Then the pesent value of the total expenditure with a X-yearly replacement policy is given by
Then the following criterion can be used for optimum replacement policy:
(i) Do not replace if the operating cost of next period is less than the weighted average of the previous costs. Where weights are 1, d, d2,…… respectively.
(ii) Replace if the operating cost of next period is greater than the weighted average of the previous costs.
Example 12:
A firm pays Rs. 10,000 for its automobiles. Their operating and maintenance costs are about Rs. 2500 per year for the first two years and then go up by approximately Rs. 1500 per year. When such cars be replaced? The discount rate is 10% per year.
Solution:
Here discount rate i = 0.1 and the depreciation ratio…
D = 1/1+0.1 = 0.9091
A = 10,000.
The value of G (X) can be calculated in the tabular form
Now C5 > G (4) and C4 < G (3)
Hence the optimum length of time to hold the machine before replacing it is 4 years.
II. Replacement of Items that Fail Completely and are Expensive to be Replaced:
In such situation the items are assumed to have relatively constant level of efficiency until they completely fail. Here replacement strategy is formulated in anticipation of failures due to which probability of failures are considered in analysis. A policy is formulated to balance the wasted life of items replaced before failure against the costs incurred when items completely fail.
It is a common characteristic that the probability of failure of any item in a system increases with time. The system may be such that the whole system may breakdown if any item fails. This breakdown implies loss in production, idle inventory, labour and other units of the system.
The nature of item which needs replacement may be such that immediate replacement is not available. Thus there is a necessity of formulating some appropriate replacement policy in such cases.
There are two main strategies:
(i) Individual Replacement Policy:
Whenever any item fails, it should be replaced immediately.
(ii) Group Replacement Policy:
All items are replaced after a certain period p inspite of these being in working order with a provision that if any item fails before this time p it can be replaced immediately. This approach decreases the probability of breakdown in the system.
Such policy requires two fold considerations, namely:
(a) The rate of individual replacement during the period.
(b) The total cost incurred on individual and group replacements during the chosen period.
The period for which the total cost is minimum is taken to be optimal.
The following information is required in this procedure:
(1) Probability of failure at different periods of time.
(2) Loss incurred due to these failures.
(3) Cost of individual replacements.
(4) Cost of group replacements.
The following criteria should be used:
Group replacement should be made at the end of the period if the cost of individual replacement for tth period is greater than average cost per period by the end of period t and one should not adopt a group replacement policy if the cost of individual replacement at the end of (t-1)th period is not less than the average cost per period through time(t- 1).
Example 13:
A Computer contains 10,000 resistors. When any resistor fails, it is replaced. The cost of replacing a resistor individually is Re. 1/- only. If all the resistors are replaced at the same time, the cost per resistor would be reduced to 15 paise.
The percent surviving say S (t) at the end of month and E P(t) the probability of failure during the month are:
What is the optimum replacement plan?
Solution:
The whole problem can be divided into two parts:
1. There is a policy of individual replacement.
2. There is a policy of group replacement.
It should be noted that no resistor survives for more than 6 months. Thus a resistor which has survived for 5 months is sure to fail during sixth month. We assume that the resistors failing during a month are replaced just at the end of the month.
Let Ni denote the number of resistors replaced at the end of the month.
The different values of Ni can be calculated in the following way:
N0 = Number of resistors in the beginning = 10,000.
N1 = Number of resistors being replaced by the end of 1st month = Number of resistors during the 1st month x probability that a resistor fails during 1st month of its installation.
= 10,000 x 0.03
= 300.
N2 = Number of resistors replaced by the end of second month.
= (Number of resistors in beginning x probability that these fail in 2nd month) + (Number of resistors replaced in first month x Probability that these will fail during second month)
= N0P2 + N1P1
= 10,000x 0.07 + 300 x 0.03
= 709
N3 = N0P3 + N1P2 + N2 P1
= 10,000 x 0.20 + 300 x 0.07 + 709 x 0.03
= 2042
N4 = N0P4+ N1P3+ N2P2 + N3P1
= 10,000 x 0.40 + 300 x 0.20 + 709 x 0.07 + 2042 x 0.03
= 4171.
N5 = N0P5 + N1P4 + N3P3 + N4P2 + N5P1
= 10,000 x 0.15 + 300 x 0.40 + 709 x 0.20 + 2042 x 0.07 + 4171 x 0.03
= 2030
N6 = N0P6 + N1P5 + N2P4 + N3P3 +N4P2 + N5P1
= 10,000 x 0.15 + 300 x 0.15 + 709 x 0.40 + 2042 x 0.20 + 4171 x 0.07 + 2030 x 0.03
= 2590
It can be seen from above calculations that Ni increases upto fourth-month and then decreases. It can also be seen that Ni will later tend to increase and the valve of Ni will oscillate till the system acquires a steady state.
The expected life of each resistor is
= ∑ xipi x, where xi is the month and Pi is the corresponding probability of failure.
= 1 x 0.03 + 2 x 0.07 + 3 x 0.20 + 4 x 0.40 + 5 x 0.15 + 6 x 0.15
= 4.02 months
Average number of replacements every month
= N/(mean age) = 10000/4.02
= 2487.5 – 2488 resistors.
Hence average cost of monthly Individual replacement policy
= Rs. 2488/- (the cost being Re. 1/- per resistor).
Now let us consider the policy of group replacement.
Hence the minimum cost per month is obtained by group replacement of all resistors after three months with an average cost of Rs. 2183.66 per month.