Break-Even Analysis:
Another form of financial analysis is breakeven analysis. It is a technique for finding a point at which a project will cover its costs, or break even. It is often used to make an initial decision on whether to proceed with a project. Breakeven analysis is also a technique of financial control in the sense that further analyses may be necessary as conditions change.
For example, an initial breakeven analysis may have indicated that sales of 80,000 units would be needed for a division to breakeven. Midway through the project, however, material costs could rise, anticipated demand could change, or price for the product could drop.
Any or all of these changes would alter the breakeven point. This in turn would signal to the organisation that it might wish to cancel the project to minimise losses. Hence, breakeven analysis can be used initially for decision-making and later for control.
ADVERTISEMENTS:
Break-Even Chart:
The objective of most private firms is to make profits — or at least to avoid losses. All business firms need to know at what point their sales revenue or income will permit them to meet all their obligations — fixed (contractual) and variable (non-contractual). This point is called the breakeven point. They are also interested in knowing at what point income from sales will exceed expenses, thus yielding a profit.
Break-even analysis, also known as cost-volume-profit analysis, is a useful tool that permits firms to visualize more clearly the revenue-cost relationship at different levels of output. It is based on certain concepts used in preparing a variable budget.
The objective of break-even analysis is to show diagrammatically revenues and costs to determine at what volume (of production or sales) a company’s total costs equal total revenues, leaving neither profit nor loss.
ADVERTISEMENTS:
Computing the Break-Even Point:
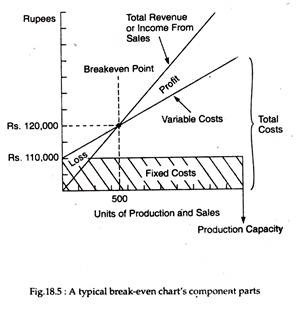
The break-even point (BEP) is the point on a chart at which total revenue exactly equals total costs (fixed and variable), Fig. 18.5 illustrates how the BEP is computed.
There are three main elements in the chart: total fixed costs, variable costs connected with each unit of production, and total revenue or income connected with each unit of production, and total revenue or income connected with each unit of sales.
ADVERTISEMENTS:
In our example total fixed cost is Rs.10,000 at all levels of output. We superimpose the total variable cost curve on the total fixed cost curve. The total revenue curve starts from the origin. It is plotted by multiplying the number of units sold by the unit price.
It intersects the total cost curve at a point which corresponds to 500 units of output. This is the break-even point, at which there is neither profit nor loss. Fig.18.7 illustrates this relationship in a simplified form.
There are different ways of calculating the BEP- Normally it is computed by dividing fixed costs by the difference between the sales price per unit and the variable cost per unit.
Break-even point (in units) = Total fixed costs/Sales price per unit – Variable cost per unit
ADVERTISEMENTS:
Suppose fixed costs are Rs.10,000 and variable costs per unit is Rs.20 for a commodity and the selling price is Rs.40.
Therefore, BEP = Rs. 10,000/Rs. 40 – Rs. 20 = 500 units as shown in Fig. 18.5.
Use of Break-Even Analysis:
Break-even analysis enables producers to determine the effect of various changes in costs and sales revenue on their availability of capital and helps them to set optimum or maximum selling prices. As a control technique, break-even analysis provides an objective measurement by which to evaluate the performance of an organisation and provides a basis for possible corrective action.
ADVERTISEMENTS:
One proximate cause of a high BEP is high investment in fixed assets. Management can locate or identify this point before deciding to invest in a new building or machine. Again, a firm may incur losses due to inadequate control of expenses. Break-even analysis can help management to detect increases in variable costs before they get out of control.
It may, however, be noted that all costs and selling prices are not entirely under the control of a procedure. Actions by competitors, suppliers, carriers, governments and changes in consumer preferences can affect costs and selling prices, as well as sales volumes at any given time. Changes in any of these variables can be plotted arid the net effect determined at a glance.
Managers can use break-even analysis to study the relationships among cost, sales volume, and profits. The break-even quantity does not remain fixed for ever. Thus output has to be shifted to the right if more profit is desired. Break-even analysis also provides a rough estimate of profit or loss at various sales volumes.
As an aid to decision making break-even analysis can;
ADVERTISEMENTS:
(i) Identify the sales volume needed to prevent a loss,
(ii) Identify the minimum production and sales volume needed to meet established objectives,
(iii) Provide data to help decide whether to add or drop a product from the product line, and
(iv) Help decide whether to raise or lower prices.
ADVERTISEMENTS:
Limitations in its use:
The very simplicity of break-even analysis is its major limitation. In practice we observe that cost and revenue functions are not linear, as specified in Fig.18.5. This is based on the assumption that variable cost per unit, total fixed costs and selling price per unit are all fixed.
But if these vary with output changes the cost and revenue functions may appear to be non-linear. In such cases we have two break points and the virtue of our analysis is partly lost.
Secondly, break-even analysis is based on the assumption that fixed and variable costs can be separated and classified. But in practice it is difficult to determine whether a cost is fixed or variable. For example, machinery is considered a fixed expense, but if it is operating at capacity and production is to be increased, it is no longer fixed.
The producer will have to buy or rent additional machinery to increase the volume of production. Also — due to wage fluctuations and changes in prices of raw materials — variable costs change greatly.
However, in spite of these difficulties, this type of analysis is valuable to management.