Theories of Exchange Rates | Foreign Exchange | Financial Management

The following points highlight the top four theories of exchange rates. The theories are: 1. Purchasing Power Parity Theory (PPP) 2. Interest Rate Parity Theory (IRP) 3. International Fisher Effect (IFE) Theory 4. Unbiased Forward Rate Theory (UFR).

1. Purchasing Power Parity Theory (PPP):

The PPP theory applies to commodities. There are two variants of the PPP: the absolute PPP theory and the relative PPP theory. PPP states that there is a link between prices in two countries and the exchange rate between the currencies of both the countries.

The theory makes three assumptions:

i. There are no transportation costs for transporting a commodity from one country to another (transportation costs are zero),

ii. There are no costs for converting one currency into another (currency conversion costs are zero).

iii. There are no restrictions on the movement of commodities between countries. That is, there are no trade barriers or quotas.

Absolute PPP Theory:

The Law of one price states that an identical product should have the same price in two countries. According to the PPP theory, the law of one price should operate for an identical commodity sold in two countries. Therefore, the price of a product in country X and the price of an identical product in country Y (in Y’s currency) should be such that, the ratio of the prices is the exchange rate between the currencies of the two countries.

When P_X is the price of a product in country X, P_Y is the price of an identical product in country Y, X is the currency of country X; and Y is the currency of country Y, then:

When the Law of one price is violated, arbitrage opportunities arise—commodities that sell at a lower price in country X will be transported to country Y (recall that transportation costs are assumed to be zero) and sold at the higher price prevailing there. This will continue till prices in both countries equalize. Absolute PPP is not relevant with respect to non-tradable goods (such as electricity, healthcare services) that cannot be transported to another country and are not traded in international markets.  

Relative PPP Theory:

When the inflation rate is higher in country X than in country Y, the price of goods in X will increase more than the price of goods in Y. Since the Law of one price states that an identical product should have the same price in both countries, X’s currency will depreciate with respect to Y’s currency. The rate of depreciation is equal to the inflation differential. Therefore, the relative version of PPP states that there is a link between the expected exchange rate E(S_n) and expected inflation rates (I) in two countries.

According to relative PPP, price changes due to differences in inflation are the cause and exchange rate changes are the effect. But if it is the other way round— that is an undervalued currency causes price change in a country—the extent of price change is termed the ‘pass through’ effect. Since the future price of a commodity is affected by the expected inflation rate, the prices of a commodity in country X and in country Y are affected by the expected inflation rates in the two countries.

When P is the commodity’s current price, and I the expected inflation rate, the price of the commodity an year later (P₁) is:

P₁ = P₀ (1 + I)

In country X – P_X1 = P_X0 (1 + I_X)

In country Y – P_Y1 = P_Y0 (1 + I_Y)

The ratio of the prices one year later is – [P_X0 (1 + I_X)] ÷ [P_Y0 (1 + I_Y)]

This can be written as S_X/Y [(1 + I_X) ÷ (1 + l_Y)] as (P_X0 ÷ P_Y0) is the current spot rate, S_X/Y. Since the expected exchange rate one year later, E(S_X/Y), is a ratio of the prices one year later, it is nothing but –  

E(S_X/Y) = S_X/Y [(1+ I_X) + (1 + I_Y )]                                     …(1)

The above equation can be rearranged as E(S _X/Y) ÷ S _X/Y = [(1 + I_x) + (1 + I_Y)]

The left hand side of this equation can be written as – 

1 + {[E(S_X/Y) – S_X/Y] ÷ S_X/Y}

where {[ E(S_X/Y) – S_X/Y] ÷ S_X/Y} is nothing but the rate of change in the spot rate.

Denoting {[E(S_X/Y) – S_X/Y]÷ S_X/Y} by ‘e’ –  

(1 + e) = [(1 + I_X) ÷ (1 + I_Y)]

On simplification, e = (I_X – I_Y) + (1 + I_Y)

The denominator on the right hand side, (1 + I_Y) can be ignored for small values of I_Y Then,

e ≈ (I_X– I_Y)                               … (2)

This equation states that e is approximately equal to (I_X – I_Y). Since e is nothing but {[E(S _X/Y) – S_X/Y] ÷ S _X/Y}, the relative PPP theory states that the rate of change in the spot rate is approximately equal to the inflation differential. When this condition holds true, the market is in equilibrium. Relative PPP is closer to reality than absolute PPP, because it accommodates non-tradable goods too—the theory talks of changes in prices (captured by changes in a price index whose composition includes non-tradable goods).

2. Interest Rate Parity Theory (IRP):

It is also called the covered interest parity theory. The theory states that there is a link between the nominal interest rates in two countries and the exchange rate between their currencies.

The theory applies to financial securities, and it makes the following assumptions:

i. When a currency is converted into another, or when a financial security is bought or sold, there are no costs involved. That is, transaction costs are zero.

ii. Money can freely flow between both the countries and there is full mobility of capital.

iii. An investor can choose to invest in financial securities that are denominated in the currency of the country where he resides (domestic currency-denominated financial securities) or to invest in financial securities that are denominated in the currency of a foreign country (foreign currency-denominated financial securities). If he chooses to invest in foreign currency-denominated financial securities, he will hedge his foreign exchange risk through operating in the forward market.

Based on the above assumptions, the theory states that the forward exchange rate for two currencies (F_X/Y) is determined by the current spot rate (S_X/Y), and the nominal interest rates (i_X and i_Y) in two countries.

The forward rate is:

F_X/Y = S_X/Y {[1 + i_X] ÷ [1 + i_y]}                            …(3)

Rearranging the above equation (which is similar to the equation for the expected spot rate E(S_X/Y) in relative PPP theory), gives – 

(F_X/Y – S_X/Y) ÷ S_X/Y = (i_x – i_y) ÷ (1 + i_y)

Note that the term (F_X/Y –  S_X/Y) on the left hand side of the above equation is negative when F_X/Y < S_X/Y (the forward rate is at a discount to the current spot rate). When F_X/Y > S_X/Y, it means that the forward rate is at a premium to the current spot rate. When the denominator (1 + i_F) on the right hand side of equation is ignored for small values of i_y, then equilibrium is said to exist when,

(F_X/Y – S_X/Y) ÷ S_X/Y ≈ (i_x – i_y)                            …(4)

When the left hand side of (4) is greater than the interest rate differential (i_X – i_F) , profit-making opportunities through covered interest arbitrage, exist. According to the IRP, when the quoted forward rate is identical to the forward rate calculated using equation 2, an investor will be indifferent to investing in securities denominated in domestic currency or foreign currency, if the return in either case is identical. When he is indifferent to the currency denomination of the financial securities, equilibrium exists.

If however, the quoted forward rate is not the same as the forward rate calculated using equation 2, an investor can make a profit by borrowing in one currency, converting it into another currency, investing the proceeds, and covering himself against exchange rate risk. This process is called covered interest arbitrage (CIA).

Equilibrium Condition under IRP:

The rate of change in the forward rate and the spot rate in illustration 3 was:

= (F_X/Y – S_X/Y) ÷S_X/Y

= (Rs. 45.7315 – Rs. 43) ÷ Rs. 43 = 0.0635 or 6.35%

The rate of change in the nominal interest rates was

= (i_X –  i_Y) ÷ (1 + i_y) = (0.1167 –  0.05) ÷ (1 + 0.05) = 0.0635 or 6.35%

Since these two rates are identical, there was equilibrium, and no scope for CIA.

Illustration:

The current spot rate is Rs. 43/USD. The nominal interest rates in India and the USA are 11.67% and 5% respectively; the one-year Rs/$ forward rate is Rs. 45.2500/$. An investor with a one- year holding period can borrow Rs. 43,000, or $ 1,000. Is covered interest arbitrage possible?

Solution:

Given S_X/Y = Rs 43/$,    .^.. X is India and Y is USA

F_X/Y = Rs. 45. 2500/$ i_X = 11.67%p.a i_Y = 5% p.a.

1. Find out [(F_X/Y – S_X/Y) ÷ S_X/Y] + i_Y

= [(45. 2500 – 43) + 43] ÷ 0.05 = 0.1023

2. Determine whether [(F_X/Y – S_X/Y) ÷ S_X/Y] + i_Y = i_X

Since 0.1023 < 0.1167 covered interest arbitrage is possible.

The investor would act as follows:

1. Borrow $1,000 for 1 year at 5% p.a. Amount repayable = $1,000 (1.05) = $1,050

2. Convert dollars borrowed at spot rate into rupees = $1,000 x Rs. 43 = Rs. 43,000

3. Invest in rupee-denominated securities for one year. Amount receivable = Rs. 43,000(1.1167) = Rs. 48,018.10

4. Sell rupee proceeds receivable forward at F_X/Y. He will receive –  Rs. 48,018.10 ÷ Rs. 45-2500 = $1,061.17

At the end of the year:

5. Receive rupee investment plus interest, Rs. 48,018.10

6. Honour the forward contract. Give Rs. 48,018.10 and get $1,061.17

7. Repay the dollar loan plus interest ($1,050). The profit = $1,061.17 – $1,050 = $11.70.

3. International Fisher Effect (IFE) Theory:

It is also called the uncovered interest parity theory. This theory states that the forward rate (F_X/Y) and the expected spot rate [E (S_X/Y)] will be identical because, even without covering exchange rate risk in the forward market, actions of market participants will make them equal.

When the forward rate is greater than the expected spot rate:

All market participants will sell the dollar forward, hoping to buy the dollar in the spot market at the expected spot rate on the day that the forward contract has to be honoured. When everyone sells dollars forward, the forward rate will fall until it becomes equal to the expected spot rate. At this point, profit-making opportunities disappear, and as the theory states, the forward rate (F_X/Y) and the expected spot rate E(S_X/Y) will be identical.

When the forward rate is less than the expected spot rate:

Market participants will buy the dollar forward, hoping to make a profit by selling it in the spot market at the expected spot rate on the day that the forward contract has to be honoured. When everyone buys dollars forward, the forward rate will rise until it becomes equal to the expected spot rate. At this point, profit-making opportunities disappear, and as the theory states, the forward rate (F_X/Y) and the expected spot rate E (S_X/Y) will be identical.

Thus, market actions will make the forward rate rise until it equals the expected spot rate. From the mathematical point of view, according to this theory,

E(S_X/Y) = F_X/Y

According to equation 2, [E(S_X/Y) –  S_X/Y] ÷ S_X/Y ≈ (I_X – I_Y)

and as per equation 4 (F_X/Y – S_X/Y ) ÷ S_X/Y ≈ (i_X – I_Y)

.^.. (i_X – i_Y) = (I_X – I_Y) and (i_X – I_X) = (i_Y – I_Y)

From the Fisher equation (i_X – I_X ) = r_X and (i_Y – I_Y) = r_Y

According to the International Fisher Effect, r_X = r_Y

This is called the Fisher Open Condition. It states that the real interest rates in countries are equal.

4. Unbiased Forward Rate Theory (UFR):

It states that the forward rate is an unbiased predictor of the expected spot rate because the actions of market participants make the ‘n’ period-forward rate be equal to the expected future spot rate. This is the equilibrium condition under the UFR theory where market actions will ensure that the ‘n’ period-forward rate is an ‘unbiased predictor’ of the expected spot rate ‘n’ days hence. There is an equal probability that the ‘n’ period-forward rate will be either higher or lower than the expected spot rate ‘n’ days later.

Comparison of the Fundamental Parity Conditions:

Are the theories described in this article valid? The theories are valid only if the assumptions are satisfied. The PPP theory’s assumptions are: zero transportation costs and free mobility of goods between countries. Even when the assumptions hold, demand for commodities in different countries is dependent on cultural, climatic, religious and ethnic preferences. Rice consumption in South Asia is more widespread and higher than in other parts of the world. So, an identical product faces different levels of demand in different countries.

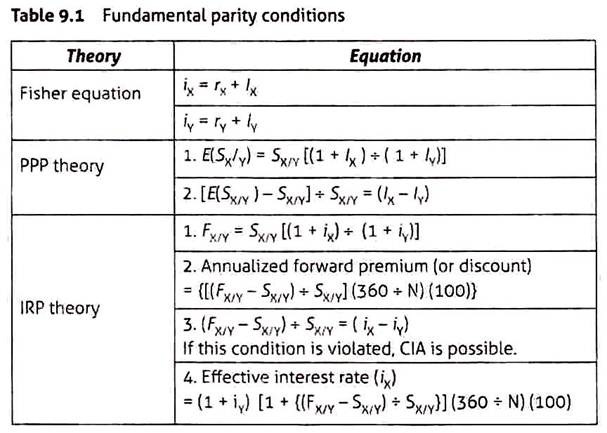
Even when a price index is used to overcome this problem, the basket of goods that form the index (index composition) varies across countries, as do the weights of individual commodities. There is substantial evidence to show that the Law of One Price does not always hold good and that domestic prices do not change in response to changes in exchange rates, and that PPP does not hold true in the short run. However, there is also empirical evidence to support at least a rough adherence to PPP theory and IRP theory in the long run. Table 9.1 gives an overview of the fundamental parity conditions.

According to the International Fisher Effect, real rates of interest between two countries should be identical. But, evidence indicates that this is not true for all countries because nominal interest rates rise and decline at different rates across countries. Between 1980 and 1985, real interest rates in the USA were higher than those in Europe, and nominal interest rates in Germany were higher than in other EU countries.

So also, Singh and Banerjee (2006) found that real interest rates in 14 emerging markets between 1991 and 2005 were not identical. The countries were Argentina, Brazil, Bulgaria, Indonesia, Korea, Malaysia, Mexico, Pakistan, Poland, Singapore, South Africa, Sri Lanka, Thailand and Turkey.

What affects the real interest rate in a country? According to IMF, the size of the fiscal deficit is critical; fiscal deficit above a certain ratio of GDP raises the real interest rate. Since countries have differing levels of fiscal deficits, the real interest rate between two countries is likely to be different.

According to the IRP theory, the forward rate is determined by the current spot rate and nominal interest rates in two countries. But there can be differences between the forward rate and the actual spot rate on that date. This occurs when the forward premium is principally a function of the demand and supply for the currencies in the spot and forward market.