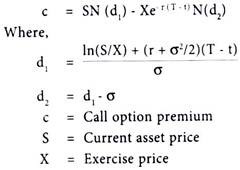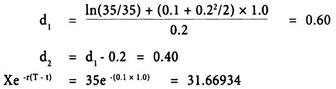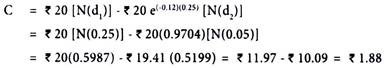Here is a term paper on ‘Options Contract’. Find paragraphs, long and short term papers on ‘Options Contract’ especially written for school and college students.
Term Paper on Options Contract
Term Paper Contents:
- Term Paper on the Definition and Meaning of Option Contracts
- Term Paper on the Kinds of Options
- Term Paper on the Features of Options
- Term Paper on the Prerequisites for Options Markets
- Term Paper on Call Option
- Term Paper on Put Option
- Term Paper on the Factors Affecting the Pricing of Options
- Term Paper on the Calculation of Premium on Options
- Term Paper on the Intrinsic Value of an Option
- Term Paper on the Time Value of Option
- Term Paper on the Marking to Market
- Term Paper on the Black and Scholes Option Pricing Model
- Term Paper on the Advantages of Options Contract
- Term Paper on the Disadvantages of Options Contract
Term Paper # 1. Definition and Meaning of Option Contracts:
ADVERTISEMENTS:
An option is the right, but not the obligation, to buy or sell something at a stated date at a stated price.
An option contract gives the holder of the contracts the option to buy or sell shares at a specified price on or before a specific Hate in the future.
The buyer of the contract pays the writer (or seller) for the right, but not the obligation, to purchase shares etc. from, or sell shares etc. to the writer at the price fixed by the contract (the striking or exercise price).
The right to choose, therefore the option, is sold by the seller (writer) of the option to the purchaser (holder) in return for a payment (premium).
ADVERTISEMENTS:
The right conveyed by the option only lasts a certain period of time and then the right expires – at its maturity or expiration.
The seller of an option has no choice.
He must meet his obligation to buy/sell if the right of the purchaser to do so is exercised at the agreed exercise/strike rate.
It is the purchaser who has choice, he does not have to exercise the right to buy/sell at the strike rate agreed if it is better from his prospective to buy/sell out spot, he can instead walk away from the option.
ADVERTISEMENTS:
In this respect options differ from futures where holders of positions do have the obligation to buy/sell the underlying asset.
At worst the purchaser will lose the premium, but can gain substantially if the option is worth exercising.
Term Paper # 2. Kinds of Options:
1. Options come in two varieties – European and American.
ADVERTISEMENTS:
2. In European option, the holder of the option can only exercise his right (if he so desire) on the expiration date.
3. In an American option he can exercise this right any time between purchase date and the expiration date.
4. Options are categorized into:
(a) Call option, and
ADVERTISEMENTS:
(b) Put option.
5. An investor who writes a call option against stock held in his portfolio is said to be selling ‘covered options’. Options sold without the stock to back them up are called ‘naked options’.
Term Paper # 3. Features of Options:
1. The option is exercisable only by the owner, namely the buyer of the option. The owner has limited liability.
ADVERTISEMENTS:
2. Owners of options have no right affordable to shareholders such as voting right and dividend right.
3. Options have high degree of risk to the option writers.
4. Options are popular because they allow the buyer profits from favourable movements in exchange rate.
5. Options involve buying counter positions by the option sellers.
ADVERTISEMENTS:
6. Flexibility in investors needs.
7. No certificates are issued by the company.
Term Paper # 4. Prerequisites for Options Markets:
1. Risk Dispersal Potential:
The contract should be capable of shifting the price risk from one party to a market participant willing to accept.
2. Volatility of the Underlying:
ADVERTISEMENTS:
The above mentioned imply that the price of the underlying must change adequately to warrant the necessity for shifting the price risk.
3. Liquidity in Trading:
In order to execute sizable orders rapidly and inexpensively there is a need to have active trading.
4. Trading Liquidity:
Active trading is needed so that sizable orders can be executed rapidly and inexpensively.
5. Underlying Standardized:
ADVERTISEMENTS:
Whatever is the underlying (be it commodity, index or security), the futures contract, need to be standardized and capable of being graded so that it is clear about the asset being bought and sold.
6. Competitive Underlying Cash Market:
The cash or physical market should be broad and efficient so that manipulations and rigging are minimized.
Term Paper # 5. Call Option:
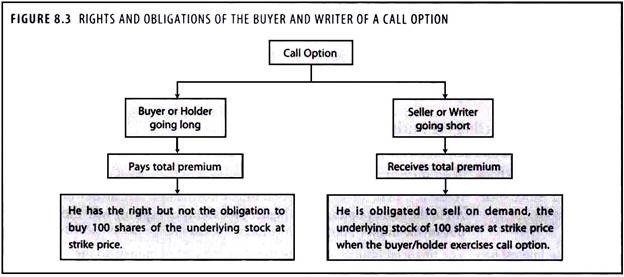
The rights and obligations of the buyer and writer of a call option are explained in Figure 8.3.
1. A call option give the buyer the right but not the obligation to buy a given quantity of the underlying asset, a given price known as ‘exercise price’ or ‘strike price’ on or before a given future date called the ‘maturity date’ or ‘expiry date’.
ADVERTISEMENTS:
2. A call option gives the buyer the right to buy a fixed number of shares/commodities in a particular security at the exercise price up-to the date of expiration of the contract.
3. The seller of an option is known as ‘writer’.
4. Unlike the buyer, the writer has no choice regarding the fulfillment of the obligations under the contract.
5. If the buyer wants to exercise his right, the writer must comply.
6. For this asymmetry of privilege, the buyer must pay the writer the option price, which is known as ‘premium’.
ADVERTISEMENTS:
ADVERTISEMENTS:
Term Paper # 6. Put Option:
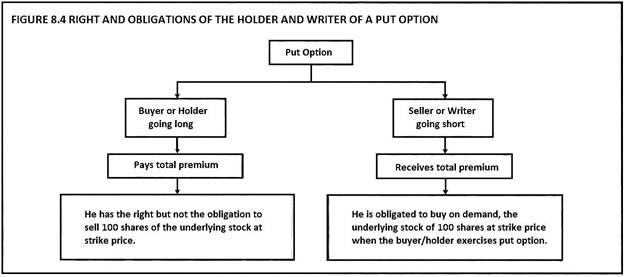
The rights and obligations of the buyer and writer of a put option are explained in Figure 8.4.
1. The put option gives the buyer the right, but not the obligation, to sell a given quantity of the underlying asset at a given price on or before a given date.
2. The put option gives the buyer the right to sell the underlying asset at the exercise price up-to the date of the contract.
3. The seller of put option is known as ‘writer’.
ADVERTISEMENTS:
4. He has no choice regarding the fulfillment of the obligations under the contract.
5. If the buyer wants to exercise his put option, the writer must purchase at exercise price.
6. For this asymmetry of privilege, the buyer of put option must pay the writer, the option price called as ‘premium’.
Term Paper # 7. Factors Affecting the Pricing of Options:
The factors that determine the premium price levels as follows:
1. Future Price:
The future price level is a major determinant of the option premium.
2. Strike Price:
Naturally, an in the-money option will be worth more than an out-of-the money option. An in the money option has a higher probability of expiring with intrinsic value than an out-of-the money option.
3. Interest Rate:
The financial futures prices are based on the cost of money, so the interest rate factor is the one of the determinants of options price.
4. Time:
The longer to expiration, the more likely are the futures to go in-the-money. The longer your car is insured, the higher the premium.
5. Volatility:
The more volatile the futures, the more likely the futures will go in-the-money or fall out- of-the money.
Term Paper # 8. Calculation of Premium on Options:
Options premium is not fixed by the exchange.
The fair value/theoretical price of an option can be known with the help of pricing models and then depending on market conditions, the price is determined by competitive bids and offers in the trading environment.
An option’s premium/price is the sum of intrinsic value and time value.
If the price of underlying stock is held constant, the intrinsic value portion of an option premium will remain constant as well.
Any change in the price of the option will be entirely due to a change in the option’s time value.
The time value component of option premium can change in response to a change in the volatility of the underlying, the time to expiry, interest rate fluctuations, dividend payments and the immediate effect of supply and demand for both the underlying and its option.
Term Paper # 9. Intrinsic Value of an Option:
The intrinsic value of an option is defined as the amount by which an option is in the money, or the immediate exercise value of the option when the underlying position is marked-to-market.
For a Call Option:
Intrinsic value = Spot price – Strike price
For Put Option:
Intrinsic value = Strike price – Spot price
The intrinsic value of an option must be a positive number or zero. It can’t be negative. For a call option, the strike price must be less than the price of the underlying asset for it to have intrinsic value. For a put option, the strike price must be greater than the underlying asset price for it to have intrinsic value.
Term Paper # 10. Time Value of Option:
The time value of an option represents the amount that options buyers are willing to pay, over and above the intrinsic value.
Options have time value because in the time between the purchase of the option and its expiration, the price of the underlying stock may change in a way favourable to the option holder.
The longer the time to expiration, the greater the time value of option.
Time value is the amount, option buyers are willing to pay for the possibility that the option may become profitable prior to expiration due to favourable change in the price of the underlying.
An option loses its time value as its expiration date nears.
At the expiration, an option is worth only its intrinsic value. Time value cannot be negative.
Term Paper # 11. Marking to Market:
Marking to market essentially means that at the end of a trading session, all outstanding contracts are repriced at the settlement price of that session, unlike the forward contracts, the futures contracts are repriced every day.
Any loss or profit resulting from repricing would be debited or credited to the margin account of the broker.
It provides an opportunity to calculate the extent of liability on the basis of repricing.
All outstanding contracts are appraised at the settlement price of that session is called as ‘marking to market’.
This means adjusting the margin accounts of both the parties.
A member incurring cost should make payment of profit to the counter party and the value of future contracts is set to zero at the end of each trading session.
The daily settlement payments are known as ‘variation margin’ payments.
Term Paper # 12. Black and Scholes Option Pricing Model:
Prof. Robert C. Metron and Prof. Myron S. Scholes have been awarded Nobel prize in Economics in 1997 for having developed a pioneering formula for the valuation of derivatives and other stock options.
In fact, they developed this method in collaboration with Prof. Fischer Black, who died in 1995.
In 1973 Black and Scholes published what has come to be known as the Black-Scholes formula.
Prof. Metron developed on this and devised another method to derive the formula that turned out to have wider applicability.
Nowadays, thousands of traders and investors use the formula every day to value of stock options in markets throughout the world.
Black, Metron and Scholes made a vital contribution by showing that it is in fact not necessary to use any risk premium when valuing an option.
This does not mean that the risk premium disappears, but that it is already rated in the stock price.
The Black-Scholes model for valuing a European call is:
Illustration 1:
The current asset price is 35.0, the exercise price is 35.0, the risk-free rate of interest is 10%, the volatility is 20% and the time to expiry is one year. Thus S = 35, X = 35, (T -t) = 1.0, r = 0.1 and σ = 0.2.
Solution:
First, we calculate d1, then d2 and, finally, the present value of the exercise price Xe-r(T – t)
Then, the equation for the call then looks like this:
c = 35N(0.6) – 31.6693N(0.4)
Here, d1 is a standardized normal random variable N(d1) is a cumulative standardized normal probability distribution. It represents the area under the standardized normal curve from Z.
By referring to mathematical table given at the end of book on the standardized normal distribution we can arrive at the values of N(d1) and N(d2) as follows:
The value of N(d1) when d1 = 0.6 is 0.7257
The value of N(d2) when d2 = 0.4 is 0.6554
When the above values are substituted in the equation, then
c = 35 (0.7257) – 31.6693 (0.6554) = 4.6434
Valuing Put Options with the Black-Scholes Model:
An alternative form of valuation is to use the Black-Scholes formula for a put, which is:
p = Xe-r(T- t)[1 -N(d2)] -S[1 -N(d1)]
Where d1 and d2 are as given in the section deriving a call option.
Note that [1 – N(d2)] is the same as N(-d2) and [1 – N(dt)] is the same as N(-d1).
Using the same data that we used in valuing the call, the put option value is calculated as follows:
p = 31.6693(0.3446) – 35(0.2743) = 1.3127
Values for d1 and d2 must be computed first, and then a table for the standard normal distribution must be used to look up the N values. In actual practice, computer algorithms and handheld calculators use a polynomial equation that will give very accurate N value approximations.
Illustration 2:
The stock options have 120 days until expiration and the strike price is Rs.85. The simple rate of interest is 6 per cent p.a. The underlying asset value is Rs.80 and the volatility (standard deviation) is 0.30. Calculate the value of the stock option.
Solution:
(1) The number of days to expiration must be converted into years by dividing by 365
Thus, t= 120/365 = 0.329
(2) The simple annual interest must be converted to the Black-Scholes continuously compounded equivalent using the relationship that 1+R = er, making r = In (1 + R).
Now r = In (1.06) = 0.0583
Now we can find the values of d1 and d2 as follows:
The next step is to lookup the N(d1) and N(d2) values in a table of such Values. Note that N(d1) = N (-0.155) and N(d2) = ( -0.327) represent areas under a standard normal distribution function. From Table given at the end of the book, we see that the value of d1 = 0.155 implies the area under the normal curve to the left of -0.155, which is approximately (interpolating from the table) .438.
The value of N(d2) is found in a similar fashion to be approximately 0.372.
Now, we can insert the above values in Black – Scholes formula, to obtain the value of the stock option.
= 80 × .438 × e(- 0. 0583 × .329) × .372 = Rs.4.03
Illustration 3:
Calculate the value of option from the following information:
Solution:
Since d1 and d2 are required inputs for Black-Scholes Option Pricing Model.
The above two represent area under a standard normal distribution function.
From table given at the end of the book, we see that value d1 = 0.25 implies a probability of 0.0987 + 0.5000 = 0.5987, so N(d1) = 0.5987. Similarly, N(d2) = 0.5199. We can use those values to solve the equation in Black- Scholes Option Pricing Model.
Assumptions of Black and Scholes Model:
In deriving their option pricing model, which calculates the value of a call option, Black and Scholes made the following assumptions:
1. The stock underlying the call option pays no dividends during the life of the option.
2. There are no transaction costs in buying or selling either the stock or the option.
3. The short-term, risk free interest rate is known constant during the life of the option.
4. Any purchaser of a security may borrow any fraction of the purchase price at the short-term, risk-free interest rate.
5. Short selling is permitted without penalty, and the short seller will receive immediately the full cash proceeds for a security sold short.
6. Trading in all securities take place in continuous time, and the stock price moves randomly in continuous time.
Valuing Embedded Options:
For listed options the Black-Scholes model can be directly applied for valuation and it is commonly used by practitioners for such a purpose.
However, for options that are not explicitly stated but embedded as part of the condition of another instrument and thus implicit, a less direct method (incorporating the standard binomial model) is commonly used by practitioners.
This mode of option valuation is used with respect to valuing the call provision for a bond.
For purposes of assessing embedded options, it is usual to view the option bearing bond as a package of cash flows and a package of options on those cash flows.
As an example, a callable bond or one that allows an issuer to redeem the bond at a specified price prior to maturity can be viewed as a package of cash flows (coupons and principal payments) and a package of call options on those cash flows.
As such the position of an investor in a callable bond can be viewed as:
Long a Callable Bond = Long an option free bond + Short a call option on the bond
Developing a value for an embedded option entails a valuation of both the bond with an embedded option and a comparable bond without an option.
The difference between these two becomes the estimated value of the embedded option.
Value of Call Option = Value of option free bond – Value of callable bond
Valuing the Callable Bond:
For a bond with an embedded option we also need to consider the like volatility of interest rates over the maturity of the bond because the cash flows to a bond with an embedded option will depend on the path that bond prices follow over the life of the bond and because the differing bond prices will depend on the volatility of interest rates.
To properly value a bond with a call provision, we need to consider the differing interest rate scenarios that might transpire over the period to maturity of the bond.
Furthermore, we can derive the implied price of the bond given the interest rate event that occurs by means of this model.
Obviously this process requires considerable programming and computer power, especially for bonds with long maturities.
Term Paper # 13. Advantages of Options Contract:
1. There is limited risk for many options strategies. The trader can lose the entire premium, but that amount is known when the position is initiated.
2. There are no margin calls for many strategies.
3. Options offer a wide range of strategies for a variety of conditions.
4. Options offer a way to add to futures positions without spending any more money or premiums. Thus, the option trader has more leverage.
5. With a forward and futures contract, the inventor is committed to a future transaction; with an option, he enjoys the right to go ahead but he can walk away from the deal if he so desires.
6. They limit the downside of risk without limiting the upside.
Term Paper # 14. Disadvantages of Options Contract:
1. The trader pays a premium to enter a market when buying options. When volatility is high, premiums can be very expensive.
2. There is more liquidity in futures contracts than there is in most options contracts. Entry and exit from some markets can be difficult.
3. There are more complex factors affecting premium prices for options. Volatility and time to expiration are often more important than price movement.
4. Many options contracts expire weeks before the underlying futures. This can be an occasional often occurs close to the final trading day of futures.
5. Option premiums don’t move tick for tick with the futures. This can be frustrating to have the market move in your direction, yet lose premium value.