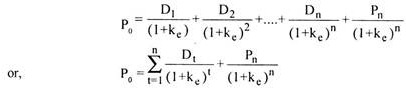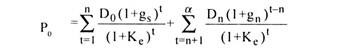Classification of Valuation Models | Financial Management

This article throws light upon the top five categories for classification of valuation models. The categories are: 1. One-Period Valuation Model 2. Two-Period Valuation Model 3. n-Period Valuation Model 4. Dividend Valuation Model 5. Earnings Capitalisation Model.

Category # 1. One-Period Valuation Model:

Suppose an investor plans to buy an equity share to hold it for one year and then sell. The value of the share for him will be the present value of expected dividend at the end of one year plus the present value of the expected sale price at the end of the year.

Symbolically:

P₀ = D₁/1 + k_e + P₁/1 + k_e

where, P₀ = Current value of the share

D₁ = Expected dividend at the end of year I

P₁ = Expected price of share at the end of year 1

K_e = The required rate of return on equity or the capitalisation/discount rate.

Illustration 10:

Mr. X is planning to buy an equity share, hold it for one year and then sell it. The expected dividend at the end of year 1 is Rs. 7 and the expected sale proceeds Rs. 200 after 1 year. Determine the value of the share to the investor assuming the discount rate of 15%.

Solution:

P₀ = D₁/(1 + k_e) + P₁/(1 + k_e)

7/1.15 + 200/1.15 = 207/1.15

= Rs. 180

Category # 2. Two-Period Valuation Model:

Suppose now that the investor plans to hold the share for two years and then sell it.

The value of the share to the investor today would be:

P₀ = D₁/(1 + k_e) + D₂/(1 + k_e)² + P₂/(1 + k_e)²

where, D₂ = Dividend expected at the end of year 2 and

P₂ = Expected Selling price at the end of year 2.

Illustration 11:

Mr. X is planning to buy an equity share, hold it for 2 years and then sell it. The expected dividend at the end of year 1 is Rs. 7 and Rs. 7.50 at the end of year 2. The expected selling price of the share at the end of year 2 is Rs. 220. Calculate the value of the share today taking 15% discount rate.

Solution:

P₀ = D₁/(1 + k_e) + D₁/(1 + k_e)² + P₂/(1 + k_e)²

= 7/1.15 + 7,50/(1.15)² + 220/(1.15)²

= Rs. 178

Category # 3. n-Period Valuation Model:

Similarly, if the investor plans to hold the share for n years and then sell, the value of the share would be:

If the expected dividend in different periods is (D) constant, we can calculate the value of the share by using annuity discount factor tables, as given below:

P₀ = (D) (ADF_i,n) + (P_n) (DF_i,n)

Illustration 12:

An investor expects a dividend of Rs. 5 per share for each of 10 years and a selling price of Rs. 80 at the end of 10 years. Calculate the present value of share if his required rate of return is 12%.

Solution:

P₀ = (D)(ADF_i,n) + (P_n)(DF_i,n)

= Rs. 5 (ADF_{12, 10}) + 80 (DF_{12, 10})

= Rs. 5(5.650) + 80 (.322)

= Rs. 28.250 + 25.760

= Rs. 54.01

Category # 4. Dividend Valuation Model:

Dividend valuation model is the generalised form of common stock valuation. The concept of this model is that many investors do not contemplate selling their share in the near future. They want to hold the share for a very long period, say infinity. In their case, the present value of the share is the capitalised value of an infinite stream of future dividends.

Some Variations in the Dividend Valuation Model:

(a) No Growth Case:

If a firm has future dividend pattern with on growth or where the dividends remain constant over time, the value of the share shall be the capitalisation of perpetual stream of constant dividends:

P₀ = D/K_e

Illustration 13:

A company is presently paying a dividend of Rs. 6 per share and is expected not to deviate from this in future. Calculate the value of the share if the required rate of return is 15%.

P₀ = D/K_e

= 6/15

= Rs. 40

(b) Constant Growth Case:

It the dividends of a firm are expected to grow at a constant rate forever, the value of the share can be calculated as:

P₀ = D₁/K_e – g = D₀ (1+g)/K_e – g

where, D₀ = Current dividend

D₁ = Expected dividend in year 1

K_e = Required rate of return on equity

g = Expected percent growth in dividend.

Illustration 14:

A company is expected to pay a dividend of Rs. 6 per share next year. The dividends are expected to grow perpetually at a rate of 9 percent. What is the value of its share if the required rate of return is 15%?

Solution:

P₀ = D₁/K_e – g

= 6/0.15 – .09 = 6/.06

= Rs. 100

Illustration 15:

The current price of a company’s share is Rs. 75 and dividend per share is Rs. 5. Calculate the dividend growth rate, if its capitalisation rate is 12 percent.

Solution:

Illustration 16:

The current price of a company’s share is Rs. 200. The company is expected to pay a dividend of Rs. 5 per share next year with an annual growth rate of 10 per cent. If an investor’s required rate of return is 12%, should he buy the share?

Solution:

Value of the share,

P₀ = D₁/K_e – g

= 5/0.12-0.10

= 5/0.02

= Rs. 250

As the value of the share (Rs. 250) is more than its current price of Rs. 200, the investor should buy the share.

Illustration 17:

The book value per share of a company is Rs. 145.50 and its rate of return on equity is 10 percent. The company follows a dividend policy of 60% pay out. What is the price of its share if the capitalisation rate is 12 percent?

Solution:

Earning per share (EPS) = 145.50 × 10/100 = Rs. 14.55

Dividend per share (D₁) = 14.55 × 60/100 = Rs. 8.73

Growth in dividend (g) = 0.10 × 40/100 = Rs. 0.04

Price of the Share, P₀ = D₁/K_e – g

= 8.73/0.12 – 0.04

= 8.73/0.08

= Rs. 109.13

(c) Supernormal Growth:

If dividends of a firm are expected to grow at a supernormal growth rate during the periods when it is experiencing very high demand for its products and then, the dividend, grow at a normal rate when the demand reaches the normal level, the constant growth equation [P₀ = D₀ (1+g)/K_e – g] has to be suitably modified to find out the present value of a share.

In case the dividends of a firm are expected to grow at a supernormal growth rate, g_s, for n years and then grow at a normal growth rate g_n, till infinity; the present value of the share can be calculated as:

The following steps are involved in solving the above equation:

(1) Calculate the present value of expected dividends during supernormal growth period.

(2) Calculate the present value of the share at the end of the supernormal growth period.

P_n = D_n+1/K_e – g_n

(3) Discount P_n back to P₀ to find out its present value at t = 0.

P₀ =P_n (1/1 + K_e)ⁿ

(4) Add the present value of expected dividends as calculated in step 1 with the present value, P₀, as calculated in step 3.

Illustration 18:

A company is currently paying a dividend of Rs. 4.24 per share. The dividend is expected to grow at a 18 percent annual rate for five years and then at 12 percent for ever. What is the present value of the share, if the capitalisation rate is 14 percent?

Solution:

Category # 5. Earnings Capitalisation Model:

When the earnings of the firm are stable or when there is an expansion situation, the value of an equity share can be determined by capitalisation of earnings. The earnings of the firm will be stable if it neither retains any earnings nor employs any external financing.

In such a situation, the retention rate, b is zero and the growth rate, br would also be zero because g= br. Further as there is no retention, dividends. D₀ will be equal to earnings E₀.

The value per share in such a case can be determined as:

P₀ = E₀(1-b)/K_e-br

or P₀ = E₀/k_e as (b = 0)

or, P₀ = D₀/k_e as (E₀ = D₀)

The expansion situation in a firm is when it has investment opportunities which will generate internal rate of return, r equal to the equity capitalisation rate, k_e (r = k_e); in such situation also

P₀ = E₀/k_e as proved below:

P₀ = E₀(1-b)/k_e-br

or, P₀ = E₀(1-b)/(k_e-bk_e)

or, P₀ = E₀(1-b)/k_e(1-b)

P₀ = E₀/K_e

Illustration 19:

Calculate the price of an equity share from the following data:

Illustration 20:

A company decides that it will not pay any dividends for 20 years. After that time it is expected that the company could pay dividend of Rs. 15 per share indefinitely. However, the company at present could pay Rs. 3 per share. The required rate of this company’s shareholders is 10 percent. What is the loss to each shareholder as a result of the policy of the company? Calculate the value of the equity share.

Solution:

The value of the share at the end of 20 years shall be:

P₂₀ = 15/10

= Rs. 150.

The current value of the share is:

P₀ = 150/(1.1)²⁰

= Rs. 22.29

The value of the share if the company at present could pay dividend of Rs. 3 per share forever:

P₀ = 3/10

= Rs. 30

Thus, the loss per share to each shareholder is:

Rs. 30—22.29 = Rs. 7.71