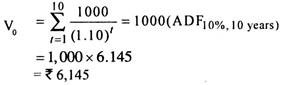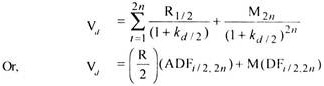After reading this article you will learn about the Valuation of Securities:- 1. Debenture Valuation 2. Share Valuation 3. Equity Share Valuation.
Debenture Valuation:
A bond is an instrument of debt issued by a business house or a government unit. The bonds may be issued at par, premium or discount. The par value is the amount stated on the face of the bond. It states the amount the firm borrows and promises to repay at the time of maturity.
The bonds carry a fixed rate of interest payable at fixed intervals of time. The interest is calculated by multiplying the value of bonds with the rate of interest.
Bond valuation is, generally, called debt valuation because the features that distinguish bonds from other debts are primarily non-financial in nature. Since bonds have a promised payment stream, they are less risky as compared to the shares. But it does not mean that they are totally risk free.
ADVERTISEMENTS:
Therefore, the required rate of return on a firm’s bond will exceed the risk free interest rate but will be less than the required rate of return on shares. The differences in required rates of return among bonds of different companies are caused by differences in ‘default risk’. The value of the bond depends upon the discount rate. It will decrease with every increase in the discount rate.
For the purpose of valuation, bonds may be classified into two categories:
(i) Bonds with a maturity period, and
(ii) Bonds in perpetuity.
ADVERTISEMENTS:
(i) Bonds with a Maturing Period:
When the bonds have a definite maturity period, its valuation is determined by considering the annual interest payments plus its maturity value.
The following formula can be used to determine the value of a bond:
where, Vd = Value of bond or debt
ADVERTISEMENTS:
R1, R2……. =Annual interest (Rs.) in period 1, 2, …, and so on
Kd = Required rate of return
M = Maturity value of bond
ADVERTISEMENTS:
n = Number of years to maturity.
It must be observed from the above equation that as n becomes large, it becomes difficult to calculate (1 + kd)n.
Symbolically:
Vd =(R)(ADFi, n) + (M)(DFi, n)
ADVERTISEMENTS:
Illustration 1:
An investor is considering the purchase of a 8% Rs. 1,000 bond redeemable after 5 years at par. The investor’s required rate of return is 10%. What should he be willing to pay now to purchase the bond?
Solution:
Bonds Redeemable in Installments:
ADVERTISEMENTS:
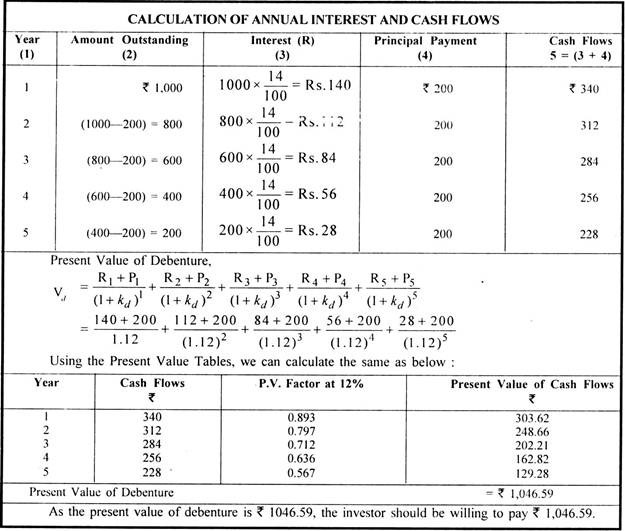
A company may issue a bond or debenture to be redeemed periodically. In such a case, principal amount is repaid partially each period instead of a lump sum at maturity and hence cash outflows each period include interest and principal. The amount of interest goes on decreasing each period as it is calculated on the outstanding amount of bond/debenture.
The value of such a bond can be calculated as below:
ADVERTISEMENTS:
Illustration 2:
A company is proposing to issue a 5 year debenture of? 1,000 redeemable in equal installments at 14 percent rate of interest per annum. If an investor has a minimum required rate of return of 12 per cent, calculate the debenture’s present value for him. What should he be willing to pay now to purchase the debenture?
Solution:
(ii) Bonds in Perpetuity:
ADVERTISEMENTS:
Perpetuity bonds are the bonds which never mature or have infinitive maturity period. Value of such bonds is simply the discounted value of infinite streams of interest (cash) flows.
where, Vd = Value or bond or debt
Kd = Required rate of return
R1 = Interest at period 1
R2 = Interest at period 2
ADVERTISEMENTS:
R = Annual Interest (as interest is constant)
Illustration 3:
Mr. A has a perpetual bond of the face value of Rs. 1,000. He receives an interest of Rs. 60 annually. What would be its value if the required rate of return is 10%?
Solution:
Vd = R/Kd
= 60/10
ADVERTISEMENTS:
= Rs. 600
Relationship between the Required Rate of Return and Coupon Interest Rate:
We have observed earlier that the value of a bond or debenture is influenced by the coupon or fixed rate of interest payable on the bond and the investor’s required or desired rate of return.
The relationship between the required rate of return and the coupon interest rate can, thus, be summarised as below:
(i) If the investor’s required rate of return and the coupon interest rate are the same, the value of the debt (bond or debenture) shall be equal to its face value or paid-up value, as the case may be.
(ii) If the required rate of return is higher than the interest rate payable on bond or debenture, the value of the bond shall be lower than its face or paid-up value.
ADVERTISEMENTS:
(iii) If the required rate of return is lower than the interest rate payable on bond or debenture, the value of the bond shall be higher than its face or paid-up value.
The above relationship can be explained with the help of following illustration.
Illustration 4:
Face value of a Debenture = Rs. 1,000
Annual Interest Rate of Debenture = 12%
Maturity Period = 5 years
ADVERTISEMENTS:
What is the value of the debenture, if:
(a) Required rate of return is 12%
(b) Required rate of return is 15%
(c) Required rate of return is 10%
Solution:
Vd = (R) (ADFi,n) + (M)(DFi,n)
Vd = 120(3.605) + 1000 (.567)
Or, Vd = 432.60 + 567
= Rs. 999.60 or say Rs. 1,000.
(b) Vd = 120 (3.352) + 1,000 (.497)
= 402.24 + 497
= Rs. 899.24
(c) Vd = 120 (3.791) + 1,000 (.621)
= 453.92 + 621
= Rs. 1075.92 or say Rs. 1076
Bond Values with Semi-Annual Interest Rates:
We have so far determined the valuation of debentures considering the annual interest payments for the sake of simplicity. However, in most of the cases, interest is payable on semi-annual or half yearly basis.
To determine the value of such bonds/debentures, the bond valuation equation has to be modified on the following lines:
(1) The annual interest amount, R, should be divided by 2 to find out the amount of half-yearly interest.
(2) The maturity period, n, should be multiplied with 2 to get the number of half yearly periods.
(3) The required rate of return, Kd, should be divided 2 to get an appropriate discount rate applicable to half-yearly periods.
Thus, the basic bond valuation equation as modified would be:
Illustration 5:
An investor holds a debenture of Rs. 100 carrying a coupon rate of 12% p.a. The interest is payable half-yearly on 30th June and 31st December every year. The maturity period of the debenture is 6 years and it is to be redeemed at a premium of 10%. The investor’s required rate of return is 14% p.a. Compute the value of the debenture.
Solution:
Vd = (R/2)(ADFi/2,2n) + M (DFi/2,2n)
12/2(7.943) + 110(.444)
47.658 + 48.840
Rs. 96.498 or say Rs. 96.50
Yield to Maturity or Bond’s Internal/Rate of Return:
We have so far assumed that the investor’s required rate of return, also called the discount rate, is given for calculating the value of the bond/debenture. However, in many cases, we may be required to calculate the required rate of return when the cash inflows and the current value/price of the bond are given.
This rate also known as ‘yield to maturity’ or ‘the internal rate of return’ for the bond can be calculated by solving the following basic equation:
Vd = R1/(1 + kd)1 + R2/(1 + kd)2 + – – – Rn/(1 + kd)n
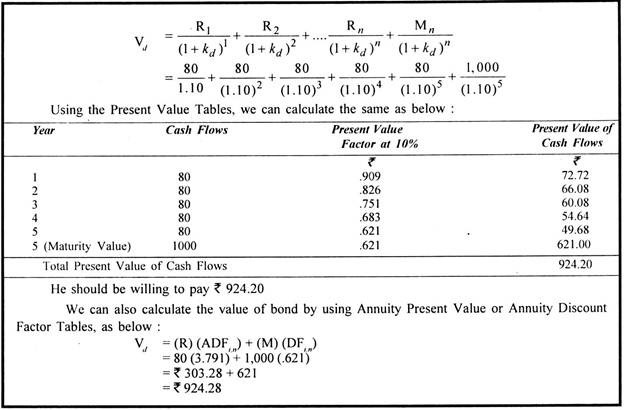
For example, suppose that the current value of a 8% debenture, of Rs. 1,000 redeemable after 5 years at par, is Rs. 924.28.
The yield to maturity or the internal rate of return can be calculated as below:
924.28 = 80/(1 + kd)1 + 80/(1 + kd)2 + 80/(1 + kd)3 + 80/(1 +kd)4 + 80/(1 + kd)5 + 1000/(1 + kd)5
We can find the value of kd equal to 10 percent from the above equation by trying several values of Kd by hit and trial method. At 10% the equation becomes:
= 80(3.791) + 1000(0.621)
= 303.28 + 621
= 924.28
However, the approximate value of yield to maturity can also be found by using the following simple formula:
Ydm = I + (F-V)/n/0.4F + 0.6V
where, I = Annual interest payment
F = Face value of bond/debenture
V = Current value/price of bond
n = Number of years to maturity
Thus, in the above example, the yield to maturity can be calculated as:
Ydm = 80 + (1000-924.28)/5)/(4/10 × 1000) + (6/10 × 924.28)
= 95.14/954.57
= 10% (appx.)
In case of perpetual or irredeemable bonds/debentures, the yield to maturity can be calculated by using the following simple equation:
Vd = R/kd or kd = R/Vd
where Vd = Value of debenture
R = Annual interest payment
kd = Required rate of return or yield to maturity.
Illustration 6:
Mr. A has a perpetual bond of the face value of Rs. 1000. He receives an interest of Rs. 60 annually. Its current value is Rs. 600. What is the yield to maturity?
Solution:
Vd = R/kd
or kd = R/Vd
or kd = 60/600 = .10
Thus, the yield to maturity is 10%.
Valuation of Zero Coupon/Deep Discount Bonds (DDBs/ZCBs):
The deep discount bond does not carry any interest but it is sold by the issuer company at deep discount from its eventual maturity (nominal) value. The Industrial Development Bank of India (IDBI) issued such DDBs for the first time in the Indian capital market at a price of Rs. 2700 against the nominal value of Rs. 1,00,000 payable after 25 years.
Since there is no intermediate payment of interest between the date of issue and the maturity date, these DDBs may also be called zero coupon bonds (ZBBs).
The valuation of a deep discount bond can also be made in the same manner as that of the ordinary bond or debenture. The only point to remember is that there shall be only one cashflow at the time of maturity in case of a deep discount bond.
Thus, the value of a DDB may be taken as equal to the present value of this future cashflow discounted at the required rate of return of the investor for number of years equal to the life of the bond.
The following formula can be used to determine the value of a DDB:
Vddb = FV/(1+rn)
where Vddb = Value of a deep discount bond
FV = Face value of DDB payable at maturity
r = Required rate of return
n = Number of years to maturity/Life of DDB.
We can also make use of the present value tables to simplify our calculations.
Symbolically:
Vddb = (FV) x (DFi,n)
Illustration 7:
A deep discount bond (DDB) is issued for a maturity period of 20 years and having a face value of Rs. 1,00,000. Find out the value of the DDB if the required rate of return is 10%.
Solution:
Vddb = FV/(1+r)n = (FV) × (DFi,n)
= 1,00,000/(1 + .10)20
= (1,00,000) × (.14864)
= Rs. 14,864.
Share Valuation:
Preference share is a hybrid security having features of both equity and debt. A fixed rate of dividend is paid on preference shares. Dividend on preference share is payable out of profits after paying interest on debt but before paying dividend on equity shares.
A preference share is also preferred in repayment as compared to equity share. Thus, preferred share is more risky than the bond but less risky than the equity share. The required rate of return on preferred stock is, therefore, greater than that of bonds.
Preferred stock or share can be with a maturity period or redeemable after a certain period or with perpetuity having no maturity period. The valuation of a preference share is very much similar to the valuation of a bond. The following formulas can be applied to find the value of the an preference share.
Value of a Redeemable Preference Share:
Vd = d/(1 +kp)1 + d/(1 + kp)2 + … … … d/(1 +kp)n Pn/(1 +kp)n
where, Vp = Value of preference share
d = Annual dividend per preference share
Pn = Maturity or redemption price of preference share
Kp = Required rate of discount on preference share.
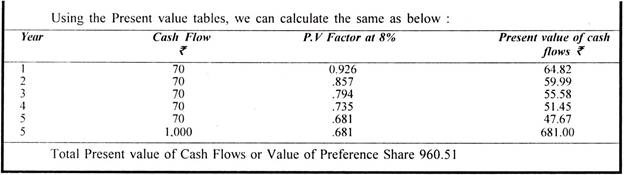
Illustration 8:
Mr. A is considering the purchase of a 7% preference share of Rs. 1,000 redeemable after 5 years at par. What should he willing to pay now to purchase the share assuming that the required rate of return is 8%?
Solution:
Value of a Perpetual Preference Share:
If the preference share has no maturity date or is irredeemable and the future dividends are expected to be constant, the value can be calculated as below:
Vp = d/kp
where, Vp = Value of preference share
d = Constant annual dividend
kp = Required rate of discount or return on preference share.
Illustration 9:
Mr. A has a irredeemable preference share of Rs. 1,000. He receives an annual dividend of Rs. 80 annually. What will be its value if the required rate of return is 10%?
Solution:
Vp = d/kp
= 80/0.10
= Rs. 800
Equity Share Valuation:
The valuation of common stock or equity shares is relatively difficult as compared to the bonds or preferred stock. The cash flows of the latter are certain because the rate of interest on bonds and the rate of dividend on preference shares are known. The cash flows expected by investors on common stock are uncertain. The earnings and dividends on equity shares are expected to grow.
However, we can determine the value of equity shares:
(i) By developing certain models based on capitalisation of dividend, and
(ii) Capitalisation of earnings. Dividend capitalisation models are the basic valuation models.