Learn how to calculate risk and return on portfolio of securities in a firm.
Return on Portfolio:
The expected return from a portfolio of two or more securities is equal to the weighted average of the expected returns from the individual securities.
Σ(RP) = WA(RA) + WB(RB)
Where, Σ(Rp) = Expected return from a portfolio of two securities
WA = Proportion of funds invested in Security A
WB = Proportion of funds invested in Security B
RA = Expected return of Security A
RB = Expected return of Security B
WA + WB = 1
Problem 1:
Anand Ltd.’s share gives a return of 20% and Vinod Ltd.’s share gives 32% return. Mr. Kumar invested 25% in Anand Ltd. shares and 75% of Vinod Ltd. shares. What would be the expected return of the portfolio.
Solution:
Portfolio Return = 0.25 (20) + 0.75 (32) = 29%
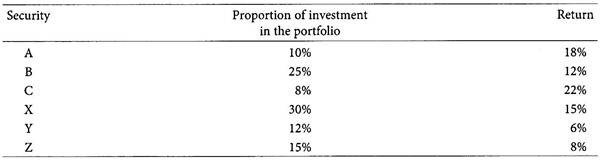
Problem 2:
Mr. Kapoor’s portfolio consists of six securities.
The individual returns of each of the security in the portfolio is given below:
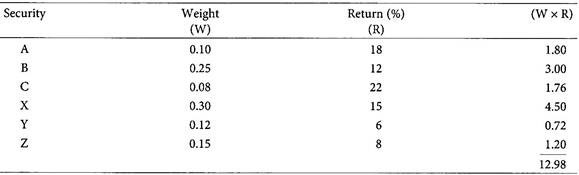
Calculate the weighted average of return of the securities consisting the portfolio.
Solution:
∴ Portfolio return is 12.98%.
Risk on Portfolio:
The risk of a security is measured in terms of variance or standard deviation of its returns. The portfolio risk is not simply a measure of its weighted average risk. The securities consisting in a portfolio are associated with each other. The portfolio risk also considers the covariance between the returns of the investment, covariance of two securities is a measure of their co-movement, it expresses the degree to which the securities vary together.
Standard Deviation of Two Share Portfolio:
(σP) = WA2σA2+WB2σB2+2WAWBρABσAσB
Where, σp = Standard deviation of portfolio consisting securities A and B
WA, WB = Proportion of funds invested in Security A and Security B
σA, σB = Standard deviation of returns of Security A and Security B
ρAB = Correlation coefficient between returns of Security A and Security B
Covariance of Security A and Security B (CovAB) = σa σR ρAB
The diversification of unsystematic risk, using two security portfolio, depends upon the correlation that exists between the returns of those two securities. The quantification of correlation is done through calculation of correlation coefficient of two securities (pAB).
The value of correlation ranges between -1 to 1, it can be interpreted as follows:
If ρAB = 1 No unsystematic risk can be diversified
If ρAB = -1 All unsystematic risk can be diversified
If ρAB = 0 No correlation exists between the returns of Security A and Security B.
Optimal Portfolio:
The investor can minimize his risk on the portfolio. Risk avoidance and risk minimization are the important objectives of portfolio management. A portfolio contains different securities, by combining their weighted returns we can obtain the expected return of the portfolio. A risk averse investor always prefer to minimize the portfolio risk by selecting the optimal portfolio.
Risk on Portfolio Consisting Three Assets:
Formula for calculating risk of portfolio consisting three securities
σp2 = Wx2σx2 + WY2σY2 + Wz2σz2 + 2WxWYρxyσxσY + 2WyWzρYZσYσz + 2WxWzρxzσxσz
Where, W1, W2, W3 = Proportion of amount invested in securities X, Y and Z
σx, σy, σz = Standard deviations of securities X, Y and Z
ρXY = Correlation coefficient between securities X and Y
ρYZ = Correlation coefficient between securities Y and Z
ρXZ = Correlation coefficient between securities X and Z