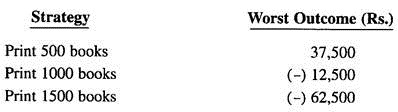In most of the decision-making situations faced by the strategy makers, a series of alternatives is available. Each alternative has some consequence depending on the occurrence or non-occurrence of some future variable or condition.
These future variables or conditions (states of nature) may be anything like the action of a competitor, the state of the economy, the state of the political system, or a technological advance.
These states of nature or condition or event are beyond a strategist’s control that could actually happen. In such a situation, a strategist has to assess the probability of occurrence of each variable and to select one of the alternatives based upon his assessment criteria.
Sensibility analysis is sometimes called ‘what if’ analysis. Sensitivity analysis, as a technique, attempts to make the strategist more aware of the ‘states of nature’ (i.e., different variables as indicated above) and of their impacts on business situations.
ADVERTISEMENTS:
It is, therefore, a method of critical assessment of decisional variables that have interrelations among them, and of identifying those sensitive variables that will have impact on the final desired result.
Recognising the fact that each individual strategist brings his or her own unique set of values, orientations, and altitudes to the decision-making process, sensitivity analysis examines a particular set of alternatives with reference to certain evaluation criteria. These criteria may relate to varying degrees of optimism or pessimism about the future or a given individual’s ability or willingness to risk losses.
In a word, sensitivity analysis involves selecting one of several alternative strategies which in combination with a future ‘state of nature’ yields some desired result. The desired result may be to maximise profit, revenue, or market share or to minimise costs, absenteeism, defective output, etc.
Procedural Steps in Sensitivity Analysis:
ADVERTISEMENTS:
1. Identify the basic underlying factors (e.g., quantity sold, unit selling price, life of project, project cost, annual cash flow, etc.)
2. Establish a relationship between the basic underlying factors (illustrated above) and net present value (or some other criterion of importance).
3. Estimate the range of variation and the most likely value of each of the basic underlying factors.
4. Study the impact on net present value of variations in the basic variables (only one factor is varied at a time).
ADVERTISEMENTS:
Merits of Sensitivity Analysis:
The merits of sensitivity analysis are:
(i) It helps to identify the underlying variables and establish interrelationships.
(ii) It shows the effect of changes of the underlying variables on a project.
ADVERTISEMENTS:
(iii) It forces the strategist to collect further information about the variable which makes the net present value more sensitive.
Demerits of Sensitivity Analysis:
The demerits of sensitivity analysis are:
(i) It is based on assumptions and assumptions pose a challenge to a strategist.
ADVERTISEMENTS:
(ii) It considers only one factor to be variable at a time, holding other factors constant and thereby, it does not give due consideration in the event of underlying factors that are interrelated.
Illustration:
Expected Value Model:
For evaluation of criteria with respect to a particular set of alternatives, in a sensitivity analysis, it is necessary to introduce the concept of expected value.
ADVERTISEMENTS:
The expected value of a given decision is the conditional value (what the event or condition is worth) times the probability of the event’s actually occurring:
For example, let us assume that a manager had a chance to invest Rs. 1, 00,000 in one of two pieces of property. Assuming, property A has a 25% chance that a new hotel if built would give a return of Rs. 50,000 and Property B has a 50% chance that an apartment if built would pay a return of Rs. 30,000, the expected values shall be:
So, a rational decision-maker would select Property B for its higher expected value.
ADVERTISEMENTS:
The philosophy behind the ‘expected value’ theory is that over the long run the decision maker will ‘do better’ to select the alternative with highest expected value. The ‘Pay-off Matrix’, for this reason, uses ‘expected value model’ to evaluate decision alternatives.
Decision-Making: Risk conditions
Conditions of risk refer to a situation in which a person (or a strategist) facing a decision problem can estimate the likelihood (i.e., probability) of a particular outcome (or result).
Decision-making under risk conditions also necessitates the use of expected values.
The expected value of an alternative is the long-run average return.
ADVERTISEMENTS:
Illustration:
Let us assume that a publisher:
(i) Has fixed the price of a book at Rs. 175, its incremental cost being Rs. 100.
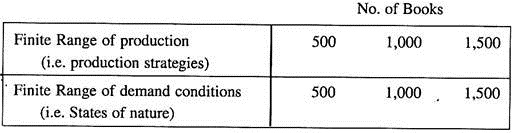
(ii) Has decided to make a sensitivity analysis within the following finite range of production and demand combinations:
Each demand level (i.e., level of sales) is a ‘State of nature’.
(iii) Has estimated the following probabilities for each demand level as:
We should, for the purpose of sensitivity analysis in respect of the above, work out:
(i) Conditional-value pay offs for production decisions, and
(ii) Expected values for production decisions.
ADVERTISEMENTS:
(i) Conditional-Value Computations:
The contribution associated with each ‘state of nature’ and ‘strategy’ is a condition value because it is conditioned on the demand for books.
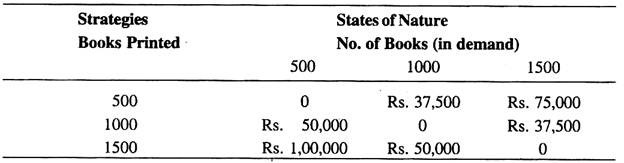
Here, contribution per book = Rs. (175 – 100) = Rs. 75, which is the actual pay off.
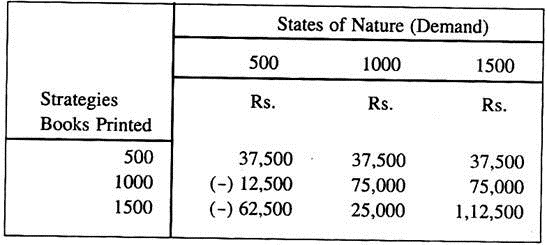
Now, Pay off associated with producing 500 books and selling 500 books = 500 x Rs. 75 = Rs. 37,500
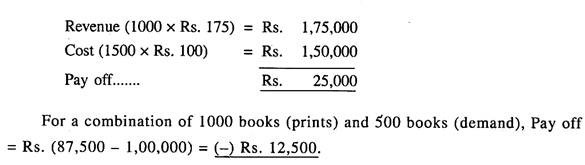
If, however, the publisher prints 1500 books and only 1000 books are in demand, the pay off is:
For a combination of 1000 books (prints) and 500 books (demand), Pay off = Rs. (87,500 – 1, 00,000) = (-) Rs. 12,500.
ADVERTISEMENTS:
For a combination of 1500 books (prints) and 500 books (demand), Pay off Rs. (87,500 – 1, 50,000) = (-) Rs. 62,500.
For a combination of 500 books (prints) and 1000 books (demand), Pay off: 500 x Rs. 75 = Rs. 37,500.
For a combination of 1000 books (both prints and demand), Pay off: Rs. (1, 75,000 – 1, 00,000) = Rs. 75,000.
For a combination of 500 books (prints) and 1500 books (demand), Pay off = 500 x Rs. (175 – 100) = Rs. 37,500.
For a combination of 1000 books (prints) and 1500 books (demand), Pay off = Rs. (1, 75,000 – 1, 00,000) = Rs. 75,000
ADVERTISEMENTS:
For a combination of 1500 (both prints and demand), Pay off = Rs. (2, 62,500 -1, 50,000) = Rs. 1, 12,500
Conditional-Value Pay Off Table:
(ii) Expected Value Computations
Expected Value = Conditional Value x Probability.
For example, the expected value for the strategy of printing 1000 books will be: (0.20 x (-) Rs. 12,500) + (0.40 x Rs. 75,000) + (0.30 x Rs. 75,000) = – 2500 + 30,000 + 22,500 = Rs. 50,000
For the strategy of printing of 500 books, the expected value will be = (0.20 x Rs. 37,500) + (0.40 x Rs. 37,500) + (0.30 x 37,500) = 7,500 + 15,000 + 11,250 = Rs. 33,750
For the strategy of printing of 1500 books, the expected value will be = (0.2 x (-) 62500) + (0.4 x 25000) + (0.30 x 1, 12,500) = – 12,500 + 10,000 + 33,750 = Rs. 31,250
Therefore, the proper decision for the publisher should be to print 1000 books as the expected value of this strategy is the highest.
Decision Making: Uncertainty Conditions:
Conditions of uncertainty refer to a situation in which a person (or a strategist) has absolutely no idea of the probabilities associated with the various alternatives being considered. In such a situation, the intuition, judgment, and personality of the strategist can play an important role.
A number of different decision criteria including the following can be used as possible bases by a strategist for decisions under uncertainty:
(i) Maximax Criterion (optimistic):
Maximising the maximum possible pay off. [Maximax Criterion refers to a choice of strategy which uses the criterion of optimism and the strategist assumes the best outcomes will occur and acts accordingly.]
A strategist with this attitude examines the conditional-value table and selects the strategy allowing the most favourable pay off. Using this criterion, the publisher would assume that no matter what strategy is selected, the best possible state of nature will occur. Therefore, the publisher should print 1500 books because that strategy is associated with the maximum pay off of Rs. 1,12,500.
But this criterion is dangerous to employ because it ignores possible losses and the chances of making or not making a profit.
(ii) Maximin Criterion (Pessimistic):
Maximising the minimum possible pay off. [Maximin Criterion refers to a choice of strategy which uses a criterion of pessimism and the strategist assumes the worst will happen and acts accordingly.]
A strategist with this attitude examines the conditional-value table and selects the strategy that maximises the least favourable pay off. Using this criterion, the publisher would find out worst possible outcomes associated with each alternative as per the conditional-value pay off table (given under: Decision making-Risk conditions), the relevant figures being:
The publisher will minimise the worst possible outcome by selecting the strategy of printing 500 books—this one is the maximum of the minimums, the best of the worst. This criterion, thus, represents an extra-conservative approach.
(iii) Minimax Criterion (Regret):
Minimising the maximum possible regret. [Minimax Criterion refers to a choice of strategy which uses the criterion of regret and the strategist acts to minimise the difference between the maximum pay off possible and the pay off for each individual alternative.]
A strategist who does not know and does not want to guess which state of nature will occur selects a regret strategy.
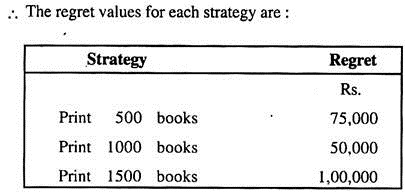
In the case of the publisher, if he prints 500 books and the demand is for 1000 books, he will experience regret of Rs. 37,500, as shown below:
The application of minimax criterion requires the development of ‘regret’ tables. These tables indicate the amount of regret associated with each strategy and state of nature.
On the basis of specimen calculation of ‘regret value’ above, the regret-value table for production decision can be presented as follows:
The minimax criterion indicates that the publisher should print 1000 books because this strategy gives the minimum regret value.
Insufficient- Reason Criterion:
Assuming equally likely probabilities for the ‘occurrence of each possible state of nature. This is also known as ‘criterion of rationality’ or ‘La Place criterion’.
[Insufficient-reason criterion refers to a choice of strategy which uses the criterion of rationality and the strategist assumes each outcome has an equal probability of occurring and acts accordingly].
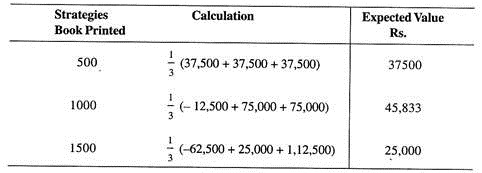
In our example for publication of books, there are three possible combinations of printing and demand; so the strategist would assign a probability of 0.33 to each strategy’s conditional-value payoffs in order to determine expected values. The table, then, appears like this:
Expected values, using Insufficient-reason Criterion.
Based on the above, the publisher should print 1000 books.
Reviewing the Choices (Under: Uncertainty Conditions):
The application of the four criteria to the decision faced by the book publisher results in different choices, depending on the orientation of the strategist, the decision-maker:
1. The optimist would print 1500 books.
2. The pessimist would print 500 books.
3. The regretter would print 1000 books.
4. The insufficient-reasoner would print 1000 books.
The greater the amount of reliable information, the more likely it is that sensitivity analysis will lead to a good decision-oriented choice of a strategy. In this respect, the decision support systems play a great role as these can provide right information at the right time for the purpose of sensitivity analysis.