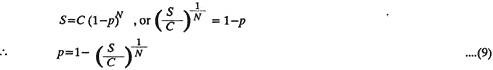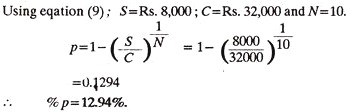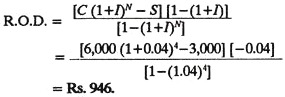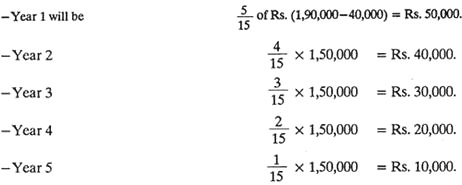The following methods may be employed for calculating depreciation of an asset: 1. Straight Line Method 2. Reducing Balance Methods 3. Production Based Methods 4. Repair Provision Method 5. Annuity Method 6. Sinking Fund Method 7. Endowment (Insurance) Policy Method 8. Revaluation Method 9. Sum of the Digits Method.
1. Straight Line Method:
This method provides for depreciation by means of equal periodic charges over the assumed life of the asset. Thus, the method is also known as the fixed installment method or proportional method. The method assumes that the fixed asset (i.e., equipment) will wear out at precisely the same rate over its useful life.
According to this method, annual depreciation charge,
A.D.C. = Rs. C-S/N …(7)
ADVERTISEMENTS:
Where
C is the original cost of the asset,
S is scrap value or residual value at the end of its useful life,
N is serviceable life in years.
ADVERTISEMENTS:
Advantages:
(i) The method is easy to understand and simple to operate.
(ii) It is frequently used in practice.
(iii) It recognises that the passing of time is a major factor in depreciation and the decline in value of an asset is directly proportional to its age.
ADVERTISEMENTS:
(iv) Uniform annual charge affords better comparative costs.
(v) The method requires little work for calculating depreciation amounts.
Disadvantages:
(i) Since fixed assets do not wear out at exactly the same rate during their life, the straight line method in many cases becomes unrealistic.
ADVERTISEMENTS:
(ii) Usually, repair and maintenance costs tend to increase in the later years of the life of an asset, it may be better to charge a higher rate of depreciation in the earlier years.
Example 1:
A melting unit for a steel foundry was purchased for Rs. 30,000. Rs. 5,000 more were spent on its erection and commissioning. The estimated residual value after ten years was Rs. 7,000. Calculate the annual rate of depreciation.
(ii) Determine the depreciation fund collected at the end of seven years after the purchase of the melting unit.
ADVERTISEMENTS:
Solution:
Using equation (7),
C = Rs. 30,000 + 5.000 = Rs.35,000
S = Rs. 7,000
ADVERTISEMENTS:
N = 10 years.
... A.D.C., Annual depreciation charge
= Rs. C-S/N =Rs. 3,500-7,000/10 = Rs. 2,800
(ii) Depreciation fund collected at the end of 7 years
ADVERTISEMENTS:
= Rs. 2,800 x 7 = Rs.19,600.
2. Reducing Balance Methods:
It is also known as Diminishing balance method or Percentage on book value method. In many cases, the cost of maintenance of an equipment i.e., fixed asset increases towards the end of its life. Therefore, it is sometimes considered desirable to calculate depreciation so that the charge lessens towards the end of the asset’s life, thus roughly equalising the combined charge of depreciation plus maintenance over the period. Reducing balance method involves non-linear change that is achieved by taking a fixed percentage, p, of the un-depreciated balance every year.
Thus at any time t, the un-depreciated portion, will be
= C. (1 –p)N ……….(8)
The method charges to the revenue account in the first year a percentage of the cost of the asset. In the following year, the same percentage will be calculated on the reduced value of the asset after the first years’ depreciation has been deducted and so on year by year until the value of the asset has been virtually reduced to nil.
Rewriting equation (8)
Advantages:
(i) It is simple to understand and calculate.
(ii) A mathematical relation can be employed to arrive at the appropriate percentage.
(iii) The method is more logical as largest annual amount of depreciation is charged in the first year when repair and maintenance charges are almost negligible.
Disadvantages:
(i) It is not simple to fix percentage, p, accurately.
ADVERTISEMENTS:
(ii) A standard percentage (p) for all conditions may produce misleading results.
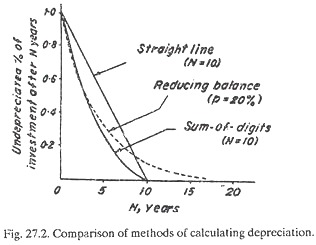
(iii) It is not possible to ever write off an amount (investment) completely by this method; it approaches the full write-off asymptotically, but never reaches it (refer Fig. 27.1).
Example 2:
An old car was purchased for Rs. 32,000. Its life was estimated as ten years and the scrap value as Rs. 18,000. Using the reducing balances method, calculate the depreciation rate (%) (b) Estimate the depreciation fund at the end of two years.
Solution:
(b) The value of car at the end of one year
C1 = C (1-p)
C1= Rs. 32,000 (1-0.1294) = RS. 27,859,20.
The depreciation fund at the end of one year
= Rs. 32,000 – Rs. 27,859.20
= Rs. 4140.80 ….(i)
ADVERTISEMENTS:
The value of car at the end of second year
C2 = C1 (1-P) = 27,859.20 (1-0.1294)
... C2 = Rs. 24,237.50.
The depreciation fund for second year
= Rs.32,000 – Rs. 24,237.50
= Rs. 3,621.70 ….(ii)
ADVERTISEMENTS:
The depreciation fund at the end of two years
= Rs. 32,000 – Rs. 24,237.50
= Rs. 7,762.50.
The same can also be obtained by adding (i) and (ii) above, i.e., Rs. 4,140.80 + Rs. 3,621.70 = Rs.7,762.50
Comparison of Reducing Balance Method with Straight Line Method:
Fig. 27.2 shows a comparison of three alternative methods of calculating depreciation:
Example 27.13 will further clarify the difference between the methods.
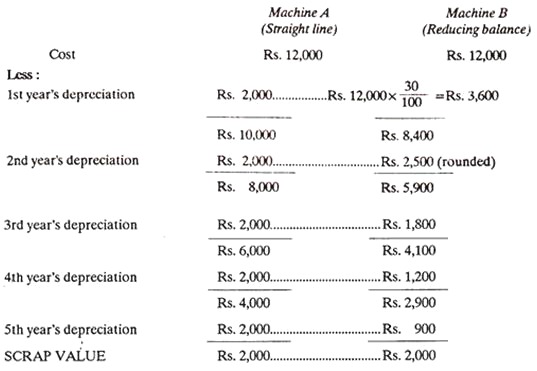
Example 3:
Two machines are purchased, each for Rs. 12,000. The estimated useful life of the machines is 5 years. The estimated scrap value is Rs. 2,000. For machined, the straight line method and for B, the reducing balance method with p = 30% is used to calculate the depreciation every year. Compare the depreciation charged in each case.
Solution:
3. Production Based Methods:
If the basis of calculation -units or hours-are to accrue at the same rate for each year, then equal installments will be charged every year. On the other hand, if output, per annum varies from one year to another (and the charge is based on the actual hours), the total annual depreciation will not be same.
Production Unit Method:
The method provides for depreciation by means of a fixed rate per unit of production calculated by dividing the value of the asset by the estimated number of units to be produced during its life.
Rate of depreciation = Value of asset/Number of units of production …(10)
Production Hour Method:
The method provides for depreciation by means of a fixed rate per hour of production calculated by dividing the value of asset by the estimated number of working hours of its life.
Rate of depreciation = Value of asset/Number of production hours …(11)
Advantages of Production Based Methods:
(i) They attempt to base depreciation on service. Instead of assuming constant depreciation every year, the hours or units in each year are estimated and depreciation is calculated.
(ii) This approach is more realistic where depreciation is determined primarily by reference to work done.
Disadvantages of Production Based Methods:
(i) It may not be easy to forecast accurately the total annual production units or hours.
(ii) These methods do not consider the fact that repair and maintenance costs tend to increase with the age of fixed assets.
Example 4:
A machine costing Rs. 2,00,000 has a residual value of Rs. 1,00,000 after 10 years of service. The estimated rate of production is 8 units per hour. Using the production unit method calculate the rate of depreciation. Assume a 50 week year and a 46 hours week.
Solution:
Using equation (10)
Rate of depreciation =2,00,000-1,00,000/10 x 50 x 46 x 8
= Re. 0.5435 per unit.
Example 5:
A machine costing Rs. 15,000 has a scrap value of Rs. 5,000 at the end of 10 years of its serviceable life. If the machine runs for 2,100 hours per-years, calculate the depreciation rate per hour of the machine and the total annual depreciation.
Solution:
Using equation (11)
Rate of depreciation per hour of machine
= Rs. 15,000 – 5,000/10 x 2,100
= Rs. 0.476
Annual depreciation = Rs. 0.476 x No. of hours per year
= Rs. 0.476 x 2,100
= Rs. 1,000.
4. Repair Provision Method:
This method is not strictly a separate method. It carries out in a more positive manner what the Reducing balance method is alleged to achieve, i.e., the equalisation of the combined charges of depreciation and repair and maintenance cost over the life of asset.
Repair and maintenance cost is added to the original cost to give a total capital outlay which is apportioned over the life of the asset. This method is often used by public works contractors as a suitable method of charging the hire and use of their own plant to contracts.
Example 6:
Cost of an air-conditioning units is Rs. 1,00,000. During an estimated life of 10 years, two major overhauls were carried out, each involving Rs, 20,000. If the scrap value of the plant is Rs. 15,000, calculate the depreciation rate on the basis of Repair provision method.
Solution:
5. Annuity Method:
It considers original cost and interest on the written down value of the fixed asset. It assumes that the purchase of a fixed asset is an investment on which interest is earned. Therefore, the investment for the purpose of the method is the written down value plus interest earned to date.
The annuity method is generally used for the redemption of leases over a fairly long period, since money invested for a lengthy period in a capital asset should be deemed to be earning interest. The mathematical relation used to calculate rate of depreciation, R.O.D., is
where C, S and N are same as in equation (7)
and I is fixed rate of interest (in fractions) determined beforehand and charged throughout the life of the asset.
Advantages:
Money invested in fixed asset is not idle, rather it is earning a certain rate of interest. Disadvantages. In most cases the interest as such never materialises. With plant, machinery and similar fixed assets, changes which take place as sales, renewals and additions tend to make the annuity method difficult to apply.
Example 7:
The cost of a machine is Rs. 6,000 and its scrap value after 4 years is Rs. 3,000. Assuming an interest rate of 4% per year find depreciation rate per year.
Solution:
Given C = Rs. 6,000
S = Rs. 3,000
N = 4 years
I = 4% = 0.04
Using equation (12)
6. Sinking Fund Method:
The method bases on the assumption of setting up a sinking fund in which money accumulates to replace the existing asset at the proper time. The method charges annually to revenue account such sum as, with compound interest, will amount to the net cost of the asset at the end of its useful life. An identical sum is charged every year as depreciation. This is invested outside the business, so that from the end of second year and each subsequent year interest is added.
At the end of useful life of the asset, the total amount in depreciation plus compound interest should become equal to the original cost of the fixed asset. This is only method so far considered which provides cash for the replacement of the asset at the end of the useful life forecast for it. The method is frequently used to provide for the amortization of leases.
The mathematical relation used to calculate annual rate of depreciation, i.e., R.O.D. is
R.O.D.= I (C-S)/ (1+I)N-1 …(13)
where I, C, S and N have same meanings as in equation (12).
Example 8:
Calculate the annual rate of depreciation from the following data, using the sinking fund method.
Cost of asset Rs. 6,000
Scrap value Rs. 3,000
Interest at the rate of 4% (compound)
Useful life period 3 years.
Solution:
Using equation (13)
R.O.D. = 0.04(6,000 –3,000)/(1 + 0.04)3– 1
= Rs. 961.
7. Endowment (Insurance) Policy Method:
The method involves charging depreciation and then investing it in the form of an endowment policy. Each year the sum charged is paid as a premium to an insurance company. At the end of the life of the asset the sum payable should be equal to the original cost.
The method is similar in effect to the sinking fund method. Cash is taken out of the business to pay the insurance premiums and is made available again at the end of the period for the purchase of another asset, when the policy matures.
8. Revaluation Method:
Revaluation method provides for depreciation by means of periodic charges, each of which is equal to the difference between the values assigned to the asset at the beginning and end of each year, for example:
“If the value of a machine on April 1,1974 is Rs. 7,000 and on March 31,1975 it is revalued as Rs. 6,000, then the depreciation for this period is Rs. 7,000 – Rs. 6,000 = Rs.1000”.
Usually the revaluation method is concerned with the recovery of original cost. The revaluation method is commonly used for loose tools, laboratory glassware, patterns, farmer’s livestock, plant used on contract work, etc.
9. Sum of the Digits Method:
The method provides for depreciation by means of differing periodic rates calculated as follows:
“If N is the estimated life of a machine, the rate is calculated for each period as a fraction in which the denominator is always the sum of the series 1, 2, 3, 4..N and the numerator for the first period is N, for second N-1, for the third N-2 and so on.”
The effect of this method is to charge depreciation at a decreasing rate each year.
Advantages:
(i) It is a method of quick depreciation for motor vehicles.
(ii) It realistically takes account of the immediate drop in value of a new vehicle, even recently purchased.
(iii) It makes the decision to sell and repurchase before the estimated time, easier.
Example 27.19 will explain the sum of the digits method.
Example 9:
The cost of a vehicle is Rs. 1,90,000. The residual (scrap) value after a period of 5 years is estimated as Rs. 40,000. Using the sum of the digits method, calculate the depreciation rate every year.
Solution:
As per the procedure of the method, the denominator will be 1 + 2 + 3 + 4 + 5 = 15, the numerators will be 5, (5-1), (5-2), (5-3) and (5-4).
Thus the depreciation charge for: