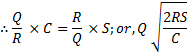The following points highlight the two important mathematical models used by a corporate strategy analyst to understand the long-term financial impact on the organisation.
Model # 1. Quantitative and Qualitative Model:
In many problems, the numerical or quantitative aspects of the various components of the problem are the most important. When we build a mathematical model and put into symbols for constants and variables, which for the most part stand for numbers, we call the result a quantitative model.
When for some problems we are concerned with qualities or properties of the elements, we use symbols for non-numerical qualities and build a mathematical model. This is termed a qualitative model. Set theory is an important source for it.
Illustrations:
ADVERTISEMENTS:
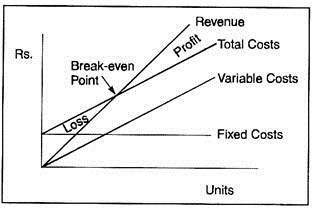
(i) Break-even analysis/Cost-volume-profit analysis is a quantitative model; yet it shows qualitative aspect.
The above model may not be useful for decision support because of certain assumptions. We might design a model that would include demand elasticity (to stimulate higher sales, lower prices), the qualitative characteristics.
ADVERTISEMENTS:
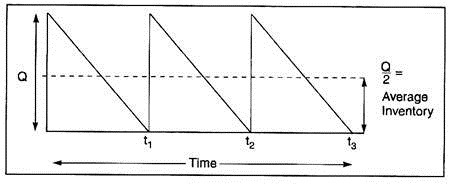
(ii) The following ‘inventory models’ are also quantitative in nature:
This average inventory model shows the arrival of Q units of inventory in stock, along with their gradual depletion over time until time t, at which the original order of Q units is totally depleted and a new order arrives. In this situation, the level of average inventory would equal Q/2. The incorporation of the element of time (t1, t2, t3 etc.) is considered a quality criterion for its practical sense.
ADVERTISEMENTS:
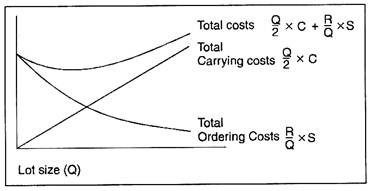
EOQ Model:
R = Total annual requirement, S = No. of orders and C = Inventory carrying costs.
At the point of intersection, carrying costs and ordering costs (Totals) are equal.
The conceptual classification of costs between inventory carrying and inventory ordering constitutes a quality criterion in its practical application.
This EOQ model can be used for determining the size of batches to manufacture a component.
When the factors of insurance, discounts, obsolescence, and deterioration of stocks are considered, the model needs adjustments no doubt but it exemplifies quality characteristics.
Model # 2. Deterministic and Probabilistic Model:
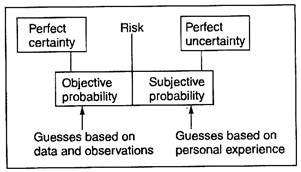
When the factors to be considered in a problem situation are within the perfect knowledge of a strategic decision maker, he becomes sure of exactness and a model in such case is deterministic.
ADVERTISEMENTS:
A model, which is based on statistics and probability and into which a decision maker introduces uncertainties/risks pertaining to real events, is called probabilistic.
This state of a strategic decision-makers knowledge ranges from perfect certainty to risk to perfect uncertainty, as diagrammed below:
Illustrations:
ADVERTISEMENTS:
The EOQ (discussed earlier) and Linear programming are deterministic models.
Linear Programming:
It is a quantitative technique used to determine the optimal mix of limited resources for maximising profits or minimising costs.
Linear Programming has the following characteristics:
ADVERTISEMENTS:
(i) It is concerned with attainment of an optimum position in relation to some objective, —usually minimisation of costs or maximisation of profits.
(ii) It involves selection among alternatives or appropriate combination of alternatives.
(iii) It takes into account certain constraints or limits within which the decision is to be arrived at. For example, the capacities of various departments are considered for optimisation of product-mix and volume-mix.
(iv) It assumes that the variables are quantifiable and that the relationships among them are linear.
Resource Allocation with Linear Programming:
Linear Programming in business finds extensive uses in resource allocation problems, and in most cases the decision support needs are recurrent.
ADVERTISEMENTS:
The problems and their elements that could be analysed, solved, and evaluated by linear programming are highlighted below:
(i) Limited resources may include investment capital, production capacity, labour, material, energy or time.
(ii) Constraints to having acceptable solutions may be anything like mandatory projects, minimum plant volumes, delivery schedules, distribution restrictions, pollution limits, demand restrictions and so on.
(iii) Problem of technology because of complex relations that exist between cost, profit, materials consumption, labour use, machine time, production volumes, energy, distribution and time.
(iv) Existence of many possible combinations in respect of products, processes, capacities, volumes, timing, storage, transportation, new facilities, etc. And each combination provides a different amounts of profit, cost, or efficiency. So, the problem is one of complexity and certainty.
ADVERTISEMENTS:
Basic Requirements for use of Linear Programming are:
(i) There must be a specified objective. For example, a steel furniture company uses one facility to produce tables, chairs, and cupboards and wants to find the most profitable product mix.
(ii) There must be alternative courses of action, each of which will achieve the objective. For example, should the company allocate production capacity between the furniture items in the ratio of 50: 25: 25: or 25: 50: 25 or 30: 60: 10 or other ratio?
(iii) Resources are in limited supply. A limited number of machine hours are available and consequently, allocation problem between the furniture items.
(iv) The variables must be interrelated. For example, if profit is Rs. 500 per table, Rs. 200 per chair and Rs. 800 per cupboard, the total profit will reflect the ratio between the items.
(v) The company’s objective and operational limitations must be expressible as linear mathematical equations or inequalities. For example, Profit (P) = Rs. 500 T + Rs. 200c + Rs. 800 CB, where T, C, and CB are the number of tables, chairs, and cupboards.
ADVERTISEMENTS:
For limited number of variables, a graphical linear programming provides a solution. But in case of many variables, a computer is frequently used for linear programming solution.
Dynamic Programming:
When the relationship between variables is not linear but continuously changing, a dynamic programming is used to solve resource allocation problems.
Dynamic programming refers to the technique of solving business problems in which resources are allocated in a sequence of interdependent decisions over a period of time, and the objective is to obtain the maximum return on the entire sequence of decisions.
Dynamic programming can be used for solving a variety of business problems, from marketing and production to financial planning. For example:
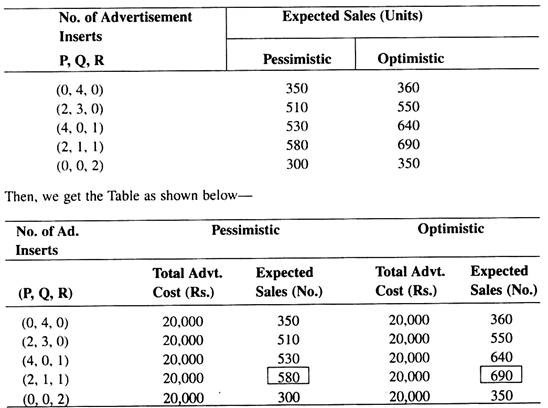
A particular market has three advertising media—P, Q, and R. Let the cost per advertisement be—P: Rs. 2500, Q: Rs. 5000, and R: Rs. 10,000. Let total advertising budget be Rs. 20,000.
ADVERTISEMENTS:
Let us also assume that the historical data reveal the following range of unit sales (optimistic to pessimistic) for each advertisement insert as follows:
According to the Table, the best course of action under either optimistic or pessimistic assumptions would be: 2 appearances in P, 1 in Q, and 1 in R.