Read this essay to learn about the three main methods of production planning in an organisation. The methods are: 1. Routing 2. Sequencing of Operations in a Production Process 3. Scheduling.
1. Essay on Routing:
According to Sprigel and Lansburg, “Routing includes the planning of where and by whom work shall be done, the determination of the path that work shall follow and the necessary sequence of operations. It forms the basis for most of the scheduling and dispatching techniques of planning.”
Kimball and Kimball also defined, “Routing to be the selection of path or route over which each piece is to travel during the process of transformation from raw material to finished product.”
In the words of H.N Broom, “Routing is a procedure of fixing the path i.e. the sequence of operations which a factory order will follow through the process”.
ADVERTISEMENTS:
It is evident from the above definitions that Routing is an important tool for production planning.
The main objective of Routing is to evolve most economical and efficient strategy so as to serve the interests of the enterprise in the best possible manner. The planner should be well acquainted with the components of production process namely, men, machines and materials to use routing procedures effectively in production planning.
The advantages of Routing can be outlined as, efficient use of available resources; reduction in production costs, improvement in the quality and quantity of output and a basis to assess the production process as well as planning for future.
2. Essay on Sequencing of Operations in a Production Process:
Sequence is an order in which a number of a jobs (operations) can be done on a finite number of service facilities (machines/equipment) in an effective manner. The measure of effectiveness can be in terms of processing time, cost of production etc. For the determination of proper sequence one should know all the operations and the order in which these can be executed to get the desired product.
ADVERTISEMENTS:
One of the common problems in production process is allocation of various operations (jobs) on machines, so as to utilise the machines in an optimum manner.
To explain the procedure of sequencing, here we shall consider only three different cases, namely:
In the system there are only two machines M1 and M2 and there are n jobs, each job is to be carried out on M1 and then on M2 .i.e., the order of the machines is M1, M2.n jobs are to be processed on three machines in the order M1, M2, M3.
(ii) n jobs are to be assigned to m machines.
ADVERTISEMENTS:
Two Machines and n Jobs:
Knowing the processing time required by each job on the machines, Johnson gave the following rules for assignment:
(i) Find the job with smallest time of processing. If this time corresponds to machine M1, then assign the job as 1st job on Ml and if this corresponds to machine M2, then assign the job as the last job on machine M2.
(ii) Remove the jobs already assigned from the candidate list and repeat step (i) to remaining jobs. Continue the process till all jobs are exhausted.
ADVERTISEMENTS:
(iii) If there are more than two jobs having same smallest time corresponding to the same machine, then the order of assignment for these jobs is arbitrary.
The method is illustrated by following examples:
Examples 1:
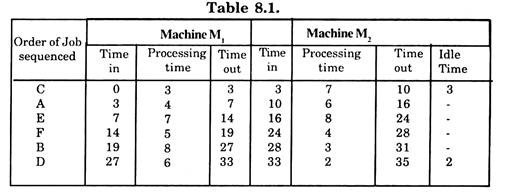
Six jobs are to be processed on two machines. The processing time for each job on each machine is given below. Find the sequence of jobs that minimises total elapsed time to complete the jobs. Also calculate the minimum elapsed time. The jobs are to be processed first on machine M1
Solution:
It is the case of two machines with six jobs and the order of the machines is M1 M2. If we see the processing times, then the minimum time is 2 for job D. on machine M2. Hence by rule 1, we assign D as last job on machine M2.
The next smallest time is 3 which is for job C on M1, and Job B on M2. Hence job C should be assigned first place in the sequence and job B the last but one place (last place already been assigned). At this stage of assignment, the following will be the position of jobs in the sequence.
Next minimum processing time is 4 for job A on M1 and job F on M2. Hence these are assigned respectively at places 2 and 4 in the sequence i.e. the sequence assignment position at this stage is
Now there is only one empty place in the sequence and one job E is left to be assigned. So job E is assigned to third place in the sequence. This completes the sequencing plan to give the order of processing as
Calculation of minimum elapsed time can be done in tubular form (8.1).
Thus the minimum processed time to complete all the jobs by the proposed sequence is 35 time units. It is also observed that total idle time for machine M2 is 5 time units. If the cycle is repeated then machine Ml will remain idle for 2 time units. Because processing of last job of previous cycle is completed i.e. after 35 time units.
Example 2:
A bookbinder has one printing press, one binding machine and the manuscript of five different books. The times required to perform the printing and binding operations for each book are known, we wish to determine the order in which books would be processed in order to minimize total time required to turn out all the books. Also find the minimum total elapsed time.
Solution:
ADVERTISEMENTS:
Evidently the order of processing will be M1, M2. Here minimum-processing time is 2 for Book II on M2. Hence Book II is to be processed last. Again next lowest time 3 corresponds to book I on M1 and IV on M2. Hence Book I is sequenced at 1st place and Book IV at 4th place. The next lowest time is 4 for Book V on M2. Thus Book V is sequenced at place 3. The required sequence of books is then.
n Jobs and Three Machines:
Let there be three machines M1, M2 and M3 and the order of processing on these machine is M1, → M2 → M3 i.e. it is M1 M2 M3 system.
The sequence of jobs in this system can be done if at least one of the following conditions is satisfied:
(i) Smallest processing time of any job on machine M1 is greater than or equal to Maximum process time of any job on machine M2 i.e. processing times of all jobs on M1 are more than the corresponding processing time of jobs on M2.
ADVERTISEMENTS:
(ii) Similarly smallest processing time of any job on M3 should be greater or equal to the maximum process time of any job on M2. If at least one of these conditions is satisfied, then for sequencing we add the processing times each job for machines M1, and M2 and also for machines M2 and M3. i.e Processing Time for Job 1 on M1 and M2 = Processing time of 1 on M1,+ Processing time of 1 on M, and Processing Time for Job 1 on M2 and M3 = Processing time of Ion M2 + Processing time of 1 on M3.
Now these two times for n jobs can be used to sequence the jobs by using the method of 8.3.1 i.e. n jobs three machines problem by this way to change into n jobs two machines problem.
Example three illustrates the use of this method.
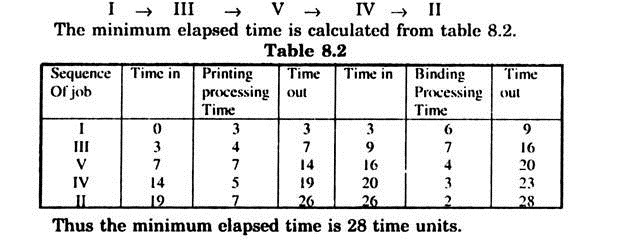
Example 3:
Find the sequence that minimises the total elapsed time (in hours) required to complete the following jobs on three machines M1 M2, M3 in the order M1, → M2 → M3.
Solution:
ADVERTISEMENTS:
Verification of the conditions:
Min time on Machine M1= 5 hours.
Max. time on Machine M2 = 5 hours.
Min. time on Machine M3 = 3 hours.
Hence, Min. time on M1, ≥ Max. Time on M2,
ADVERTISEMENTS:
Min time on M3 ≤ Max. Time on M2
So one of the conditions is satisfied.
The processing times of various jobs are now added first for M1 and M2 and then for M2 and M3 to get the following table:
Now the sequencing of the jobs can be done by the method describe in 8.3.1 considering M1, and M2 as one machine and M2 and M3 as another machine. Here minimum time is 5 for job A on M2 M3. Hence job A is processed last.
Similarly Job B has next minimum time on both M1 M2 and M2 M3 and also job E on M1 M2, also has the same minimum time. So we assign job E at 1st place and job at 2nd place. The job with next lowest time is C on M2 M3. So it is assigned at place IV.
ADVERTISEMENTS:
The remaining Job D is assigned 3rd place to get the sequence as:
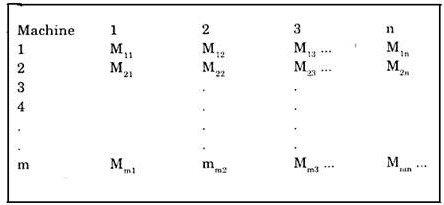
n Jobs and m Machines:
Let the processing times of each job on each machine be given following tabular form:
i.e. Mij is the processing time of jth job on Machine i.
Here i = 1, 2,…… , m and j = 1, 2,……… , n. The order of processing be on machinesl, 2, 3, …., m.
Now solution of the problem is possible if following conditions are satisfied.
(i) At least one of min. of Mij (for allj), min of Mij (for all j) is greater than or equal to max. of M2j, Max M3j,…. Max of Mm-1 j for all j.
(ii) If sum of processing times (Mi2 + Mi3 + Mim. 1) is constant for all machines. Then sequencing of jobs can be done by considering the processing times of machines 1 and m only.
The method is illustrated by the following example:
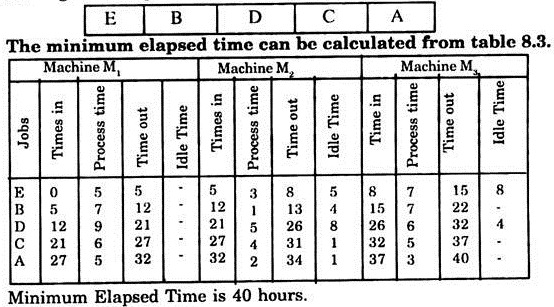
Example 4: Solve the following sequencing problem:
Order of Processing being M1 M2 M3 M4
Solution:
We find that:
Minimum processing time on M1 is 8.
Minimum processing time on M4 is 7.
Minimum processing time on M2 is 5.
Minimum processing time on M3 is 7.
Hence, Min. Mj ≥ Max M2j, Max.M3j.
Min. M4j ≥ Max. M2j, Max. 3j.
So condition (i) is satisfied. The problem is reduced to two machine problem by adding the processing times M1j +M2j +M3j and M4j+M2j+M3j for each job and solving the problem by the method described in 8.3.1.
Alternative method:
If we add the processing times of machines M2 and M3 for each job, we find that the sum for all jobs is same i.e.8.
So for this problem sequencing can be done by considering M, and M4 only i.e. consider it as 2-machine problem i.e.:
Using method of 8.3.1 the optimal sequence again is
Assignment of n Candidates on n Jobs:
Let there be n candidates or workers and each is to be assigned some job. The performance of the person varies with the job he is assigned. Let eij denote the measure of performance for ith candidate on jth job. Evidently i = 1, 2, ……… n for candidates and j=1 to n for jobs.
The assignment algorithm consists of following steps:
(i) The values e showing the effective measure of performance are written in the formij of a matrix E.
eij‘s can be in terms of costs, times etc.
For minimisation problem.
(ii) (a) Find the minimum element of each row and subtract it from all the elements of that row.
(b) Find the minimum element of each column of the matrix obtained after step (a) and subtract it from the elements of that column.
(iii) Draw minimum element of Horizontal and Vertical lines passing through all zero’s of the matrix obtained in step (ii). This can be done by
(a) Locate the rows/ columns which contain maximum number of uncovered zeros (Say X) and draw covering line through every line having X uncovered zero’s.
(b) See whether all zeroes are covered or not. If not then go to step (a) otherwise go to step(c).
(c) Let Y be the number of zeros covered by a line which are not also covered by a second covering line. If Y=0 then remove the covering line otherwise go to next covering line.
(iv) Count the number of horizontal and vertical lines covering all zero’s in step.(iii).
Let it be z. (a) if Z=n then the stage of optimum assignment has reached. (b) If z ǂ n, then go to step (v).
(v) Select the smallest element out of those elements which are not covered by the lines in step (iv). Subtract this element from the remaining uncovered elements and add this element to those elements which lie on the intersection of horizontal and vertical lines in step (iv) and go to step (iv). Continue the process till the stage of Optimum solution arrives i.e. Z = n, and then go the solution identification routine in step(vi).
(vi) Consider only the zeroes of the performance matrix obtained in step v and examine all the rows (column) one by one to find one with exactly unmarked zero.
Encircle this zero and cross the remaining zeros in its column (row). If there is any unmarked zero left then encircle this zero to get the optimum solution.
There may be situations that an optimal solution for an assignment problem exists but one may find the number and positions of the zero cell in the final matrix to be such that more than one optimal assignment can be made. The indication of such situation is that during the process of assignments via the final matrix, arrow or column that contains only one zero cannot be located. This is known as situation of Multiple Optimal Solutions. Here encircle one of the unmarked zero arbitrarily and cross the remaining zero’s in that row and column.
Note:
In the case of maximization problem, all the elements of the cost matrix are multiplied by -1 and then the above algorithm can be applied i.e. maz z = – min (-z).
Example 5:
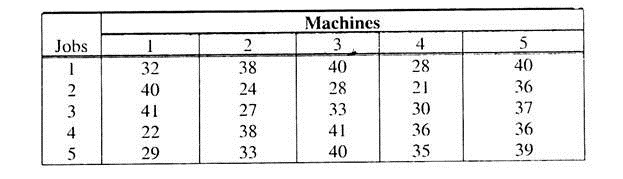
Five jobs are to be processed and five machines are available. Any machine can process any job and the resulting profits are given in the following matrix form.
What is the maximum profit with an optimum assignment?
Solution:
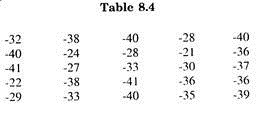
This is a maximization problem. So it is converted into a minimization problem by multiplying all the elements of cost matrix by -1 and then applying the steps of assignment algorithm.
So we get Table 8.4.
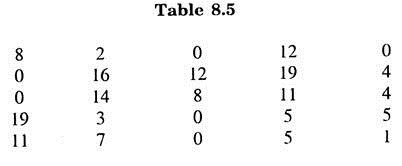
(a) Subtracting minimum elements of each row (-40, -40, -41, -41 and -40) from the elements of that row, we get Table 8.5.
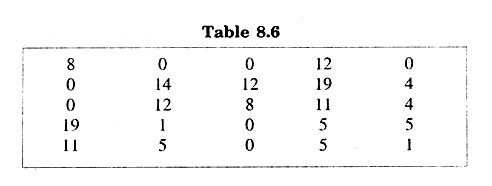
Subtract minimum element of each column (0, 2, 0, 5, 0) of Table 8.5 from the elements of that column to get table 8.6.
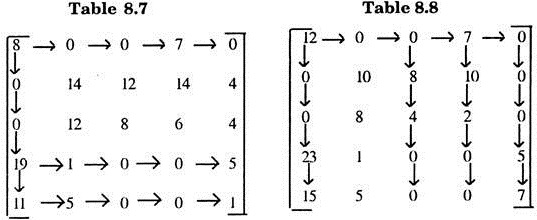
Apply Step II on Table 8.6. to get Table 8.7.
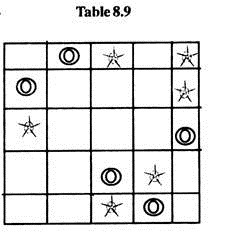
In table 8.7 N = 4 which is less than n=5, Hence the stage of optimal assignment is not there. So we apply step (v). The minimum of elements uncovered by the lines in Table 8.7 is 4. We subtract it from the uncovered elements and add it to the elements lying on the cross-section of horizontal and vertical lines in Table 8.7 and again Apply step(iv) to get Table (8.8).
In table (8.9) N = 5 = n. Hence this is the stage of optimal solution.
Now we consider only the zeros in table (8.9).
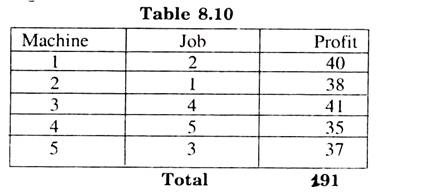
(i) In column II of table 8.9.There is only one zero so we encircle it and cross the remaining zero’s in that Row.
(ii) In row II of (8.9) we encircle zero In 1st column and cross the other zero’s in 2nd row and first column.
(iii) There is only one zero left unmarked in 3rd row, so it is encircled.
(iv) In fourth row we encircle the zero in column (3) and cross the other zeros in that row and column.
(v) The unmarked zero’s in Table (8.9) provide the required optimum assignment plan given in Table 8.10.
(vi) The encircled zero’s in table (8.9) provide the required optimum assignment plan given table 8.10
So total profit with optimum assignment plan will be Rs. 191.
3. Essay on Scheduling:
Once the sequence of operations is finalized, the production planning department should try to fix the starting and finishing time for each operation with an object to achieve maximum utilisation of resources i.e. men, machines and capital, so that men and machines are not idle.
The preparation of this plan is known as Scheduling. Thus scheduling is to specify the time and the sequence in which the operations in a production process are to be executed. In the words of Sprigel and Lansburg, “Scheduling involves establishing the amount of work to be done and the time when each element of work will start or the Order of the work.”
According to Kimball and Kimball, “The determination of time that should be required to perform each operation and also the time that should be required to perform, the entire series as routed, is scheduling.”
The factors on which scheduling depends are, the manufacturing system, amount of output, handling and transportation requirements, procurement time etc.
Thus Routing covers ‘where’ and Scheduling covers ‘when’ aspects of production planning.